If (-1, -1) and (3, -1) are two opposite corners of a square, the other two corners a
(2, 0), (- 2, 2)
(2, -2), (0, 2)
(3,0), (4, - 2)
None of these
The correct Answer is:D
To find the other two corners of the square given the opposite corners (-1, -1) and (3, -1), we will follow these steps:
Step 1: Identify the given points
The two opposite corners of the square are:
- Point A: (-1, -1)
- Point B: (3, -1)
Step 2: Find the midpoint of the diagonal
The midpoint of the diagonal can be calculated using the midpoint formula:
Midpoint=(x1+x22,y1+y22)
Substituting the coordinates of points A and B:
Midpoint=(−1+32,−1+(−1)2)=(22,−22)=(1,−1)
Step 3: Determine the slope of the line segment AB
The slope of the line segment connecting points A and B can be calculated as:
Slope=y2−y1x2−x1=−1−(−1)3−(−1)=04=0
This indicates that the line segment AB is horizontal.
Step 4: Find the coordinates of the other two corners
Since the square is oriented such that its sides are perpendicular to the line segment AB, the other two corners will be vertically aligned with the midpoint. The distance from the midpoint to each corner is equal to half the length of the diagonal.
The length of the diagonal AB can be calculated as:
Length of AB=√(x2−x1)2+(y2−y1)2=√(3−(−1))2+(−1−(−1))2=√(4)2+(0)2=4
Thus, half the length of the diagonal is 2.
Step 5: Calculate the coordinates of the other corners
The other two corners will be located 2 units above and below the midpoint (1, -1):
- Corner C: (1, -1 + 2) = (1, 1)
- Corner D: (1, -1 - 2) = (1, -3)
Final Answer
The other two corners of the square are:
- Corner C: (1, 1)
- Corner D: (1, -3)
---
The two opposite corners of the square are:
- Point A: (-1, -1)
- Point B: (3, -1)
The midpoint of the diagonal can be calculated using the midpoint formula:
Midpoint=(x1+x22,y1+y22)
Substituting the coordinates of points A and B:
Midpoint=(−1+32,−1+(−1)2)=(22,−22)=(1,−1)
The slope of the line segment connecting points A and B can be calculated as:
Slope=y2−y1x2−x1=−1−(−1)3−(−1)=04=0
This indicates that the line segment AB is horizontal.
Since the square is oriented such that its sides are perpendicular to the line segment AB, the other two corners will be vertically aligned with the midpoint. The distance from the midpoint to each corner is equal to half the length of the diagonal.
Length of AB=√(x2−x1)2+(y2−y1)2=√(3−(−1))2+(−1−(−1))2=√(4)2+(0)2=4
Thus, half the length of the diagonal is 2.
The other two corners will be located 2 units above and below the midpoint (1, -1):
- Corner C: (1, -1 + 2) = (1, 1)
- Corner D: (1, -1 - 2) = (1, -3)
The other two corners of the square are:
- Corner C: (1, 1)
- Corner D: (1, -3)
Topper's Solved these Questions
- COORDINATE GEOMETRYBOOK - DISHA PUBLICATIONCHAPTER - COORDINATE GEOMETRYEXERCISE - EXPERT LEVEL
28 Videos
- COORDINATE GEOMETRYBOOK - DISHA PUBLICATIONCHAPTER - COORDINATE GEOMETRYEXERCISE - TEST YOURSELF
15 Videos
- COORDINATE GEOMETRYBOOK - DISHA PUBLICATIONCHAPTER - COORDINATE GEOMETRYEXERCISE - FOUNDATION LEVEL
65 Videos
- AVERAGESBOOK - DISHA PUBLICATIONCHAPTER - AVERAGESEXERCISE - Test Yourself
15 Videos
- FUNCTIONSBOOK - DISHA PUBLICATIONCHAPTER - FUNCTIONSEXERCISE - Test Yourself
15 Videos
Similar Questions
Knowledge Check
If (0, -1) and (0, 3) are two opposite vertices of a square, then the other two vertices are
A(0, 1), (0, -3)B(3, -1), (0, 0)C(2, 1), (-2, 1)D(2, 2), (1, 1)The point (1,3) and (5,1) are two opposite vertices of a rectangle. The other two vertices lie on the line y=2x+c, then the other vertices and c are
A(1,1)(2,3)B(4,4),(2,0)C(0,0),(5,4)DnoneA(1,3)andC(7,5) are two opposite vertices of a square. The equation of a side through A is
Ax+2y−7=0B2x+y−5=0Cx−2y+5=0D2x−y+1=0
If A(3, 4) and C (1, -1) are two opposite angular points of square ABCD, find the coordinates of other two vertices.
View SolutionIf (2,1),(−2,5) are two opposite vertices of a square; then the area of the square is
View SolutionA(1,3)andC(7,5)are two opposite vertices of a square. The equation of a side thro' A is
View SolutionTwo equal positive charges are placed at two corners or a square, 'the' other two corners having neglative charges or equal magnitude. Find the field intensity in the centre of the square in the two cases.
View SolutionTwo point charges of +q each are placed at two diagonally opposite corners of a square. Another two point charges of -q charge each are placed at the two remaining corners. Take the edge length of square equal to l. Calculate (i) work needed to move these charges slowly from an infinite separation to this given configuration. (ii) Assume that four charges at corners of the square are held fixed. Another charge Q is to be moved from infinity to the centre of this square slowly. What additional work is required to do so?
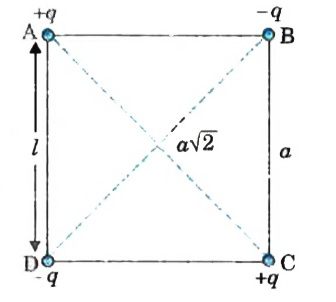
View Solution
