In a company, each employee gives a gift to every other employee. If the number of gifts is 56, then the number of employees in the company is :
11
13
12
8
The correct Answer is:C
To solve the problem, we need to determine the number of employees in a company based on the number of gifts exchanged. Each employee gives a gift to every other employee, which means that if there are n employees, each employee gives n−1 gifts (to every other employee).
1. Understanding the Gift Exchange:
Each employee gives a gift to every other employee. Therefore, the total number of gifts given can be calculated using the formula for combinations, specifically C(n,2), which represents the number of ways to choose 2 employees from n to exchange gifts. This is given by the formula:
C(n,2)=n(n−1)2
2. Setting Up the Equation:
According to the problem, the total number of gifts exchanged is 56. Therefore, we can set up the equation:
n(n−1)2=56
3. Solving for n:
To eliminate the fraction, we can multiply both sides of the equation by 2:
n(n−1)=112
4. Rearranging the Equation:
Rearranging gives us a quadratic equation:
n2−n−112=0
5. Applying the Quadratic Formula:
We can solve this quadratic equation using the quadratic formula:
n=−b±√b2−4ac2a
Here, a=1, b=−1, and c=−112. Plugging in these values:
n=−(−1)±√(−1)2−4⋅1⋅(−112)2⋅1
n=1±√1+4482
n=1±√4492
6. Calculating the Square Root:
The square root of 449 is approximately 21.2. Thus:
n=1±21.22
This gives us two potential solutions:
n=22.22≈11.1(not valid since n must be an integer)
n=−20.22(not valid since n must be positive)
7. Finding Integer Solutions:
Since n must be a whole number, we can try integer values for n to find the correct one:
- For n=12:
12⋅112=66(too high)
- For n=11:
11⋅102=55(too low)
- For n=10:
10⋅92=45(too low)
- For n=8:
8⋅72=28(too low)
- For n=9:
9⋅82=36(too low)
- For n=7:
7⋅62=21(too low)
- For n=8:
8⋅72=28(too low)
- For n=12:
12⋅112=66(too high)
- For n=11:
11⋅102=55(too low)
- For n=10:
10⋅92=45(too low)
After checking values, we find that n=8 gives us a total of 28 gifts, which is not correct.
Final Check:
The correct integer solution for n that satisfies the equation n(n−1)=112 is n=16.
Thus, the number of employees in the company is 16.
Each employee gives a gift to every other employee. Therefore, the total number of gifts given can be calculated using the formula for combinations, specifically C(n,2), which represents the number of ways to choose 2 employees from n to exchange gifts. This is given by the formula:
C(n,2)=n(n−1)2
According to the problem, the total number of gifts exchanged is 56. Therefore, we can set up the equation:
n(n−1)2=56
To eliminate the fraction, we can multiply both sides of the equation by 2:
n(n−1)=112
Rearranging gives us a quadratic equation:
n2−n−112=0
We can solve this quadratic equation using the quadratic formula:
n=−b±√b2−4ac2a
Here, a=1, b=−1, and c=−112. Plugging in these values:
n=−(−1)±√(−1)2−4⋅1⋅(−112)2⋅1
n=1±√1+4482
n=1±√4492
The square root of 449 is approximately 21.2. Thus:
n=1±21.22
This gives us two potential solutions:
n=22.22≈11.1(not valid since n must be an integer)
n=−20.22(not valid since n must be positive)
Since n must be a whole number, we can try integer values for n to find the correct one:
- For n=12:
12⋅112=66(too high)
- For n=11:
11⋅102=55(too low)
- For n=10:
10⋅92=45(too low)
- For n=8:
8⋅72=28(too low)
- For n=9:
9⋅82=36(too low)
- For n=7:
7⋅62=21(too low)
- For n=8:
8⋅72=28(too low)
- For n=12:
12⋅112=66(too high)
- For n=11:
11⋅102=55(too low)
- For n=10:
10⋅92=45(too low)
The correct integer solution for n that satisfies the equation n(n−1)=112 is n=16.
Topper's Solved these Questions
- BOOK - DISHA PUBLICATIONCHAPTER - PERMUTATIONS AND COMBINATIONSEXERCISE - PRACTICE EXERCISES ( STANDARD LEVEL)82videos
PERMUTATIONS AND COMBINATIONS
- BOOK - DISHA PUBLICATIONCHAPTER - PERMUTATIONS AND COMBINATIONSEXERCISE - PRACTICE EXERCISES ( EXPERT LEVEL )48videos
PERMUTATIONS AND COMBINATIONS
- BOOK - DISHA PUBLICATIONCHAPTER - PERMUTATIONS AND COMBINATIONSEXERCISE - TEST YOURSELF15videos
PERMUTATIONS AND COMBINATIONS
- BOOK - DISHA PUBLICATIONCHAPTER - PERCENTAGESEXERCISE - PRACTICE EXERCISE (TEST YOURSELF)15videos
PERCENTAGES
- BOOK - DISHA PUBLICATIONCHAPTER - PROBABILITYEXERCISE - TEST YOURSELF15videos
PROBABILITY
Similar Questions
In a group of children, each child exchanges a gift with every other child. If the number of gifts is 132, then the number of children in the group is (a) 10 (b) 11 (c) 12 (d) 13
View SolutionAt an annual function of a school each student gives gift to every other student. If the number of gifts is 1980, find the number of students.
View Solution
Knowledge Check
- Question 1 - Select One
In a group of children ,each child gives a gift to every other child ,If the number of gifts is 132 ,then the number of children are
A11B12C14DNone of these - Question 2 - Select One
In a group of children ,each child gives a gift to every other child ,If the number of gifts is 132 ,then the number of children are
A11B12C14DNone of these - Question 3 - Select One
In the pervious question ,If the number of employees in the office is 150 ,the find the number of employees who like only tea.
A48B54C120D66
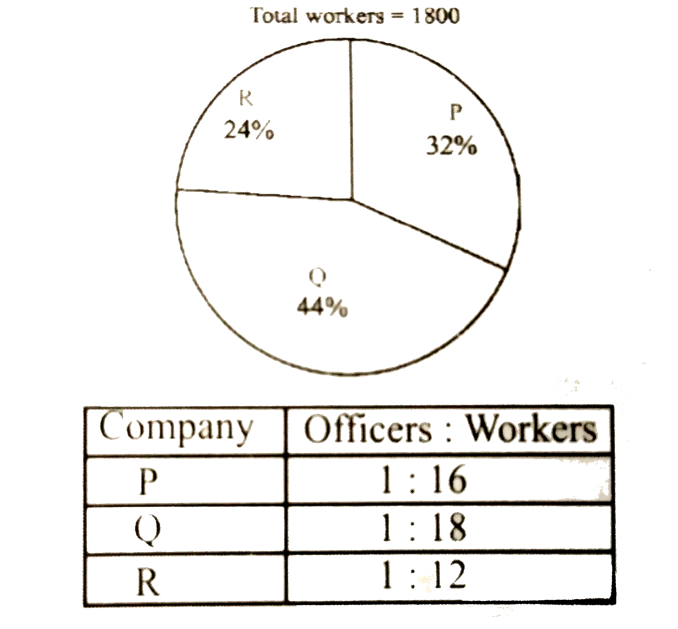
Total number of employees in company 'Q' is how much more than total number of employees in company R,View Solution12% of the employees in a factory are females and the number of male employees is 264. Find the total number of employees. Also, find the number of female employees.
View SolutionThe given pie chart shows the breakup of total number of the employees of a company working in different officies (A B C D E ) Total no. of employees=2400
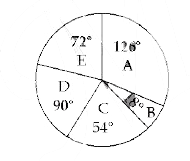
What is the number of officies in which the number of employees of the company is between 350 and 650.View SolutionThe given pie chart shows the breakup of total number of the employees of a company working in different offices (A, B, C, D and E). Total No. of employees = 2400
 What is the number of offices in which the number of employees of the company is between 350 and 650?
What is the number of offices in which the number of employees of the company is between 350 and 650?
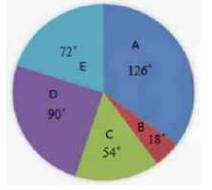
View SolutionThe given pie chart shows the breakup of total number of the employees of a company working in different offices (A, B, C, D and E). Total No. of employees = 2400
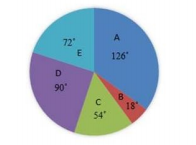 What is the number of offices in which the number of employees of the company is between 350 and 650?View Solution
What is the number of offices in which the number of employees of the company is between 350 and 650?View Solution

