A,B,C,D and E are coplanar points and three of them lie in a straight line. What is the maximum number of triangles that can be drawn with these points as their vertices?
p2(4p−3)
p3(4p−3)
p(4p−3)
p3
The correct Answer is:A
Step by step video, text & image solution for A,B,C,D and E are coplanar points and three of them lie in a straight line. What is the maximum number of triangles that can be drawn with these points as their vertices? by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Topper's Solved these Questions
- BOOK - DISHA PUBLICATIONCHAPTER - PERMUTATIONS AND COMBINATIONSEXERCISE - TEST YOURSELF15videos
PERMUTATIONS AND COMBINATIONS
- BOOK - DISHA PUBLICATIONCHAPTER - PERMUTATIONS AND COMBINATIONSEXERCISE - PRACTICE EXERCISES ( STANDARD LEVEL)82videos
PERMUTATIONS AND COMBINATIONS
- BOOK - DISHA PUBLICATIONCHAPTER - PERCENTAGESEXERCISE - PRACTICE EXERCISE (TEST YOURSELF)15videos
PERCENTAGES
- BOOK - DISHA PUBLICATIONCHAPTER - PROBABILITYEXERCISE - TEST YOURSELF15videos
PROBABILITY
Similar Questions
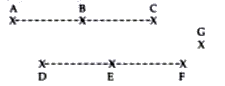
How many maximum numbers of triangles can be formed with the seven points A, B, C, D, E, F, and G ?View SolutionTwo straight lines intersect at a point O. Points A1,A2...,An are taken on one line and points B,B2,...,Bn, on the other. If the point O is not to be used, then the number of triangles that can be drawn using these points as vertices, is
View Solution
Knowledge Check
- Question 1 - Select One or More
There are p coplanar parallel lines. If any 3 points are taken on each of the lines, the maximum number of triangles with vertices at these points is:
A3pC3−pB9P2(p−1)2C4P2(P−1)D18PC2+27PC3 - Question 2 - Select One
There are 10 points in a plane. No three of these points are in a straight line. What is the total number of straight lines which can be formed by joining the points?
A90B45C40D30 - Question 3 - Select One
Answer these questions based on the following informations
Two parallel lines each have a number of distinct points marked on them. On one line there are two points P and Q. On the other line there are eight points
Find the maximum number of different triangles which could be formed having three of the ten points as their verticesA3B2C64D6
There are 10 points on a straight line AB and 8 on another straight line AC, none of them being A. How many triangles can be formed with these points as vertices?
View SolutionThere are 10 points in a plane out of which 5 are collinear. The number of straight lines than can be drawn by joining these points will be
View SolutionThere are 15 points in a plane, no three of which are in a straight line except 4, all of which are in a straight line. The number of triangles that can be formed by using these 15 points is:
View Solution4 points out of 11 points in a plane are collinear. Number of different triangles that can be drawn by joining them, is
View SolutionThere are n points in a plane, No three being collinear except m of them which are collinear. The number of triangles that can be drawn with their vertices at three of the given points is
View Solution

