Consider the following in respect of the matrix A=[−111−1] :
1. A2=−A
2. A3=4A
Which of the above is/are correct ?
Only 1
Only 2
Both 1 and 2
Neither 1 nor 2
To solve the problem, we need to verify the two statements given for the matrix A=(−111−1).
Step 1: Calculate A2
To find A2, we multiply matrix A by itself:
A2=A×A=(−111−1)×(−111−1)
Calculating the elements of A2:
- First row, first column:
(−1×−1)+(1×1)=1+1=2
- First row, second column:
(−1×1)+(1×−1)=−1−1=−2
- Second row, first column:
(1×−1)+(−1×1)=−1−1=−2
- Second row, second column:
(1×1)+(−1×−1)=1+1=2
Thus, we have:
A2=(2−2−22)
Step 2: Calculate −A
Now, we calculate −A:
−A=−(−111−1)=(1−1−11)
Step 3: Compare A2 and −A
Now we compare A2 and −A:
A2=(2−2−22)and−A=(1−1−11)
Since A2≠−A, Statement 1 is incorrect.
Step 4: Calculate A3
To find A3, we can use the result from A2:
A3=A2×A=(2−2−22)×(−111−1)
Calculating the elements of A3:
- First row, first column:
(2×−1)+(−2×1)=−2−2=−4
- First row, second column:
(2×1)+(−2×−1)=2+2=4
- Second row, first column:
(−2×−1)+(2×1)=2+2=4
- Second row, second column:
(−2×1)+(2×−1)=−2−2=−4
Thus, we have:
A3=(−444−4)
Step 5: Calculate 4A
Now, we calculate 4A:
4A=4×(−111−1)=(−444−4)
Step 6: Compare A3 and 4A
Now we compare A3 and 4A:
A3=(−444−4)and4A=(−444−4)
Since A3=4A, Statement 2 is correct.
Conclusion
- Statement 1: Incorrect
- Statement 2: Correct
Thus, the answer is that only Statement 2 is correct.
---
(−1×−1)+(1×1)=1+1=2
- First row, second column:
(−1×1)+(1×−1)=−1−1=−2
- Second row, first column:
(1×−1)+(−1×1)=−1−1=−2
- Second row, second column:
(1×1)+(−1×−1)=1+1=2
(2×−1)+(−2×1)=−2−2=−4
- First row, second column:
(2×1)+(−2×−1)=2+2=4
- Second row, first column:
(−2×−1)+(2×1)=2+2=4
- Second row, second column:
(−2×1)+(2×−1)=−2−2=−4
- Statement 2: Correct
Topper's Solved these Questions
Similar Questions
Consider the following inequalities in respect of any triangle ABC :
1. AC−AB<BC
2. BC−AC<AB
3. AB−BC<AC
Which of the above are correct ?
View SolutionConsider the following in respect of the matrix:
⎡⎢⎣111111111⎤⎥⎦
1. Inverse of A does not exist.
2. A3=A
3. 3A=A2
Which of the above are correct?
View Solution
Knowledge Check
Consider the following in respect of a complex number Z :
1. ¯¯¯¯¯¯¯¯¯¯¯(Z−1)=(¯¯¯Z)−1
2. ZZ−1=|Z|2
Which of the above is/are correct?A1 onlyB2 onlyCBoth 1 and 2DNeither 1 nor 2Which one of the following is correct in respect of the matrix ?
⎡⎢⎣00−10−10−100⎤⎥⎦ ?AA. A−1 does not existBB. A=(-1) ICC. A is a Zero matrixDD. A2=1The rank of the matrix A=[12344321], is
A1B2C3D4
Consider the matrix A=[2345].
Hence , find A−1.
View SolutionConsider the following statements in respect of the matrix A=⎡⎢⎣012−10−3−230⎤⎥⎦
I. The matrix A is skew symmetric
II. The matrix A is symmetric
III. The matrix A is invertible
Which of the above statements is/are correct ?
View Solution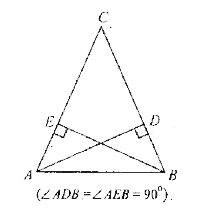
Consider the following in respect of the above figure :
1. △DAC~△EBC
2. CA/CB = CD/CE
3. AD/BE = CD/CE
Which of the above are correct ?
View SolutionConsider the following :
1. sin1∘>sin1c
2. cos1∘<cos1c
3. tan1∘>tan1c
Which of the above are not correct ?
View SolutionConsider the following statements in respect of the matrix A=⎡⎢⎣012−10−3−230⎤⎥⎦
1. The matrix A is skew-symmetric.
2. The matrix A is symmetric.
3. The matrix A is invertible.
Which of the above statements is/are correct ?
View Solution
