Curve of intersection of two spehere is
an ellipse
a circle
a parabola
None of these
The correct Answer is:B
To determine the curve of intersection of two spheres, we can follow these steps:
Step 1: Understand the Geometry of Spheres
A sphere in 3D space is defined by its center and radius. The equation of a sphere with center (h,k,l) and radius r is given by:
(x−h)2+(y−k)2+(z−l)2=r2
We can have two spheres, S1 and S2, with their respective equations.
Step 2: Set Up the Equations
Let’s assume the equations of the two spheres are:
- Sphere S1: (x−h1)2+(y−k1)2+(z−l1)2=r21
- Sphere S2: (x−h2)2+(y−k2)2+(z−l2)2=r22
Step 3: Find the Intersection
To find the intersection of the two spheres, we can subtract one equation from the other. This will eliminate the quadratic terms and lead us to a linear equation in x, y, and z:
(x−h1)2+(y−k1)2+(z−l1)2−(x−h2)2−(y−k2)2−(z−l2)2=r21−r22
Step 4: Analyze the Resulting Equation
The resulting equation will represent a plane in 3D space. The intersection of this plane with either of the spheres will yield a curve.
Step 5: Identify the Type of Curve
The intersection of a plane with a sphere is a circle. Therefore, the curve of intersection of two spheres is a circle.
Conclusion
Thus, the curve of intersection of two spheres is a circle.
---
A sphere in 3D space is defined by its center and radius. The equation of a sphere with center (h,k,l) and radius r is given by:
(x−h)2+(y−k)2+(z−l)2=r2
We can have two spheres, S1 and S2, with their respective equations.
Let’s assume the equations of the two spheres are:
- Sphere S1: (x−h1)2+(y−k1)2+(z−l1)2=r21
- Sphere S2: (x−h2)2+(y−k2)2+(z−l2)2=r22
To find the intersection of the two spheres, we can subtract one equation from the other. This will eliminate the quadratic terms and lead us to a linear equation in x, y, and z:
(x−h1)2+(y−k1)2+(z−l1)2−(x−h2)2−(y−k2)2−(z−l2)2=r21−r22
The resulting equation will represent a plane in 3D space. The intersection of this plane with either of the spheres will yield a curve.
The intersection of a plane with a sphere is a circle. Therefore, the curve of intersection of two spheres is a circle.
Thus, the curve of intersection of two spheres is a circle.
Topper's Solved these Questions
Similar Questions
The equations of two curves are y2=2x and x2=16y (A) The angle of intersection of these curves is π2 (B) The angle of intersection of these curves is tan(35) (C) The equation of common tangent to these curve is x+2y+2=0 (D) The equation of common tangent to these curves is x+2y−2=0
View SolutionIf the equation of two curve is y2=4axandx2=4ay
(i) Find the angle of intersection of two curves.
(ii) Find the equation of common tangents to these curves.
View Solution
Knowledge Check
Curve of intersection of two spheres in
Aan ellipseBa circleCa parabolaDNone of theseAt the point of intersection of the two curves shown, the conc. of B is given by ……… for, A→nB:
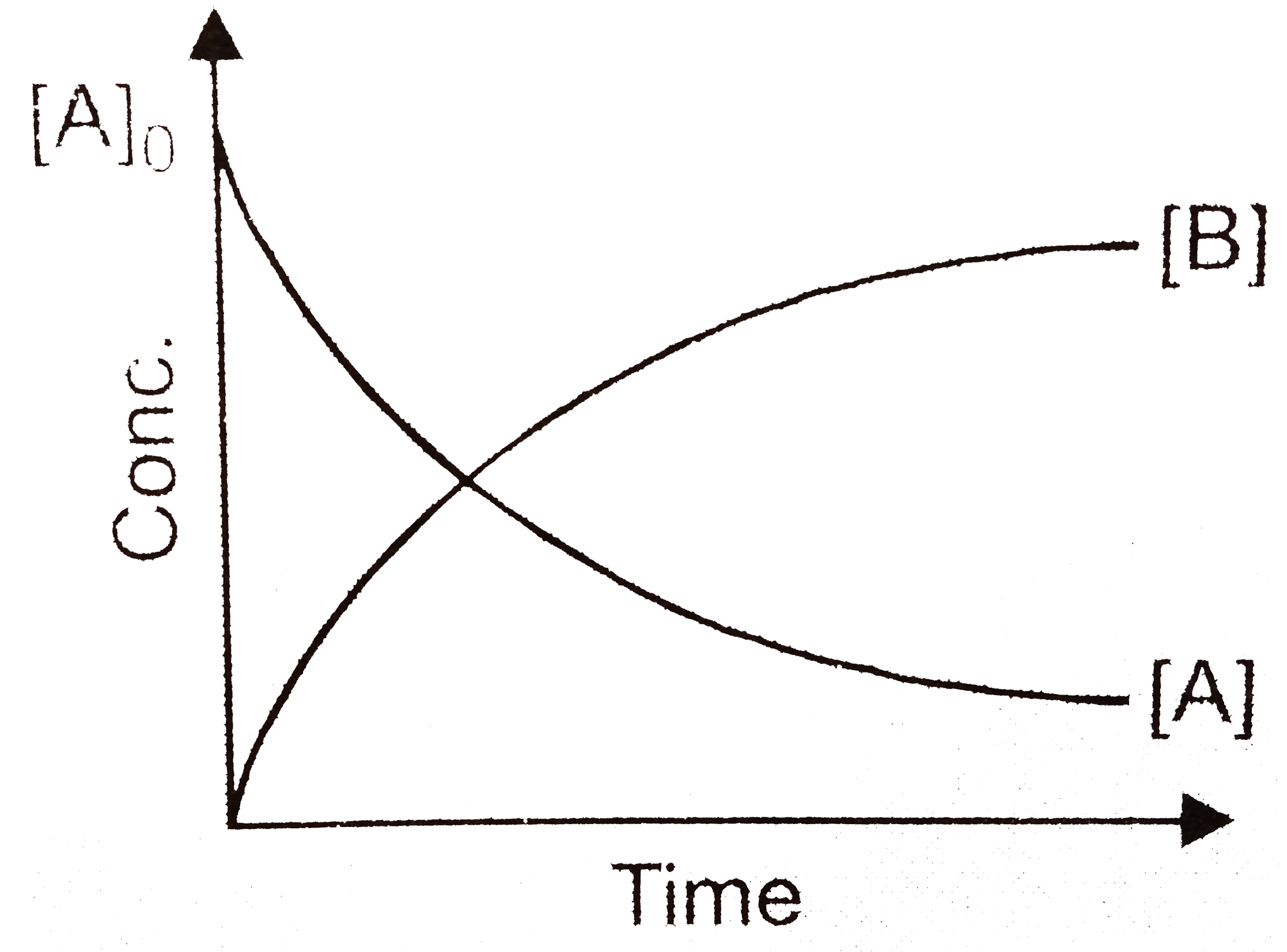 AnA02BA0n−1CnA0n+1D(n−1n+1)A0
AnA02BA0n−1CnA0n+1D(n−1n+1)A0At the point of intersection of the two curves shown, the conc.of B is given by….. ….. ……….for, A→nB
 AnA02BA0n−1CnA0n+1D(n−1n+1)A0
AnA02BA0n−1CnA0n+1D(n−1n+1)A0
Angle of intersection of two circle and orthogonal intersection of circles
View SolutionThe number of point of intersection of the two curves y = 2 sin x and y = 5x2+2x+3 is :
View SolutionThe points of intersection of the two curves |z−3|=2 and |z|=2 in an argand plane are:
View SolutionThe number of points of intersection of the two curves y=2sinxandy=5x2+2x+3 is
View SolutionAt the given point of intersection of the two curves shown concentration of B is given by ………for, A=3B
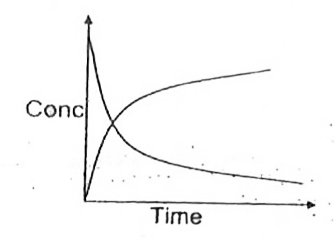
View Solution
