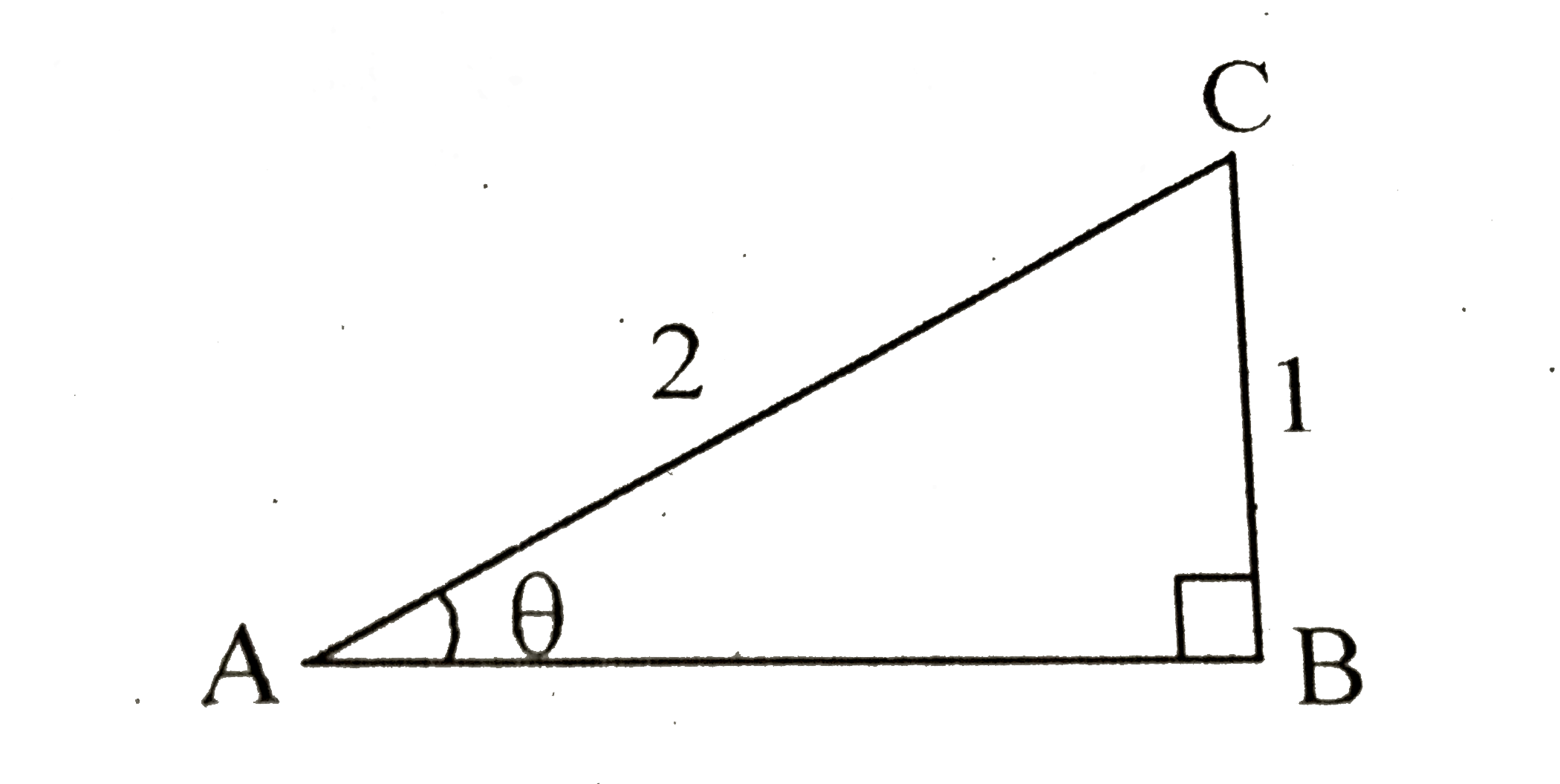
In ΔABC,∠B=90∘andAB:BC=2:1 .Then value of sin A+cot C is
3+√5
2+√52√5
2+√5
3√5
The correct Answer is:B
To solve the problem, we need to find the value of sinA+cotC in triangle ΔABC where ∠B=90∘ and the ratio AB:BC=2:1.
1. Identify Triangle Dimensions:
Since AB:BC=2:1, we can assign lengths to the sides. Let:
- AB=2k (opposite to angle C)
- BC=k (opposite to angle A)
2. Calculate the Hypotenuse:
Using the Pythagorean theorem, the hypotenuse AC can be calculated as:
AC=√(AB)2+(BC)2=√(2k)2+(k)2=√4k2+k2=√5k2=k√5
3. Find sinA:
The sine of angle A is given by the ratio of the opposite side to the hypotenuse:
sinA=BCAC=kk√5=1√5
4. Find cotC:
The cotangent of angle C is given by the ratio of the adjacent side to the opposite side:
cotC=ABBC=2kk=2
5. Combine sinA and cotC:
Now we can find sinA+cotC:
sinA+cotC=1√5+2
6. Combine into a Single Fraction:
To combine these, we can express 2 as a fraction:
2=2√5√5
Therefore,
sinA+cotC=1√5+2√5√5=1+2√5√5
Final Answer:
Thus, the value of sinA+cotC is:
1+2√5√5
Since AB:BC=2:1, we can assign lengths to the sides. Let:
- AB=2k (opposite to angle C)
- BC=k (opposite to angle A)
Using the Pythagorean theorem, the hypotenuse AC can be calculated as:
AC=√(AB)2+(BC)2=√(2k)2+(k)2=√4k2+k2=√5k2=k√5
The sine of angle A is given by the ratio of the opposite side to the hypotenuse:
sinA=BCAC=kk√5=1√5
The cotangent of angle C is given by the ratio of the adjacent side to the opposite side:
cotC=ABBC=2kk=2
Now we can find sinA+cotC:
sinA+cotC=1√5+2
To combine these, we can express 2 as a fraction:
2=2√5√5
Therefore,
sinA+cotC=1√5+2√5√5=1+2√5√5
Thus, the value of sinA+cotC is:
1+2√5√5
Topper's Solved these Questions
- TRIGONOMETRY BOOK - KIRAN PUBLICATIONCHAPTER - TRIGONOMETRY EXERCISE - TYPE -III
90 Videos
- TRIGONOMETRY BOOK - KIRAN PUBLICATIONCHAPTER - TRIGONOMETRY EXERCISE - TYPE -IV
22 Videos
- TRIGONOMETRY BOOK - KIRAN PUBLICATIONCHAPTER - TRIGONOMETRY EXERCISE - TEST YOURSELF
25 Videos
- TIME AND WORKBOOK - KIRAN PUBLICATIONCHAPTER - TIME AND WORKEXERCISE - TEST YOURSELF
25 Videos
Similar Questions
Knowledge Check
In ΔABC,∠B=90∘andAB:BC=2:1. The value of of sinA+cotC is
A3+√5B2+√52√5C2+√5D3√5In ΔABC,∠C=90∘andAB=c,BC=a,CA=b , then the value of cosec B-cos A) is
Ac2abBb2caCa2bcDbca2In ΔABC,BC=ABand∠B=80∘. Then, ∠A=?
A50∘B40∘C100∘D80∘
See the gven figure. In ΔABC,∠B=90∘,∠A=30∘,AC=14, then findAB and BC.
View SolutionInΔABC,∠B=90∘andcosA=941, then find all other trigonometric ratios for ∠B.
View SolutionIn a ΔABC,∠B=90∘,AB=7cmand(AC−BC)=1cm, find the values of sinA,cosA,sinCandC.
View SolutionIn ΔABC,∠B=90∘ , if AB=5cm,BC=12 cm , then find the vlaues of the following :
(a) Sin A
(b) Cos A
cot A
cosec C
( e) sec C
tan C
View SolutionIn ΔABC,∠B=90∘andsinA=45, then find the values of all other trigonometric ratios for ∠A.
View Solution