The radius of circle A is twice that of circle B and the radius of circle B is twice that of circle C. Their area will be in the ratio
16:4:1
4:2:1
1:2:4
1:4:16
The correct Answer is:A
To solve the problem, we need to find the ratio of the areas of three circles (A, B, and C) based on their radii. Let's break it down step by step.
Step 1: Define the radii of the circles
Let the radius of circle C be r. According to the problem:
- The radius of circle B is twice that of circle C:
rB=2r
- The radius of circle A is twice that of circle B:
rA=2rB=2(2r)=4r
Step 2: Write down the radii
Now we have:
- Radius of circle A: rA=4r
- Radius of circle B: rB=2r
- Radius of circle C: rC=r
Step 3: Calculate the areas of the circles
The area A of a circle is given by the formula:
A=πr2
Now we can calculate the areas of each circle:
1. Area of circle A:
AA=π(rA)2=π(4r)2=π(16r2)=16πr2
2. Area of circle B:
AB=π(rB)2=π(2r)2=π(4r2)=4πr2
3. Area of circle C:
AC=π(rC)2=π(r)2=π(r2)=πr2
Step 4: Write the areas in ratio form
Now we have the areas:
- Area of circle A: 16πr2
- Area of circle B: 4πr2
- Area of circle C: πr2
To find the ratio of the areas, we can express them without the common factor πr2:
Ratio=16:4:1
Step 5: Simplify the ratio
The ratio 16:4:1 is already in its simplest form.
Final Answer
Thus, the ratio of the areas of circles A, B, and C is:
16:4:1
---
Let the radius of circle C be r. According to the problem:
- The radius of circle B is twice that of circle C:
rB=2r
- The radius of circle A is twice that of circle B:
rA=2rB=2(2r)=4r
Now we have:
- Radius of circle A: rA=4r
- Radius of circle B: rB=2r
- Radius of circle C: rC=r
The area A of a circle is given by the formula:
A=πr2
Now we can calculate the areas of each circle:
AA=π(rA)2=π(4r)2=π(16r2)=16πr2
AB=π(rB)2=π(2r)2=π(4r2)=4πr2
AC=π(rC)2=π(r)2=π(r2)=πr2
Now we have the areas:
- Area of circle A: 16πr2
- Area of circle B: 4πr2
- Area of circle C: πr2
Ratio=16:4:1
The ratio 16:4:1 is already in its simplest form.
Thus, the ratio of the areas of circles A, B, and C is:
16:4:1
Topper's Solved these Questions
- BOOK - KIRAN PUBLICATIONCHAPTER - MENSURATIONEXERCISE - TYPE - III21videos
MENSURATION
- BOOK - KIRAN PUBLICATIONCHAPTER - MENSURATIONEXERCISE - TYPE - IV169videos
MENSURATION
- BOOK - KIRAN PUBLICATIONCHAPTER - MENSURATIONEXERCISE - Test Yourself28videos
MENSURATION
- BOOK - KIRAN PUBLICATIONCHAPTER - LCM AND HCF EXERCISE - Test Yourself18videos
LCM AND HCF
- BOOK - KIRAN PUBLICATIONCHAPTER - MISCELLANEOUSEXERCISE - TYPE-VI15videos
MISCELLANEOUS
Similar Questions
Knowledge Check
- Question 1 - Select One
The ratio of circumference and radius of a circle is :
A2π:1Bπ:1C1:1DNone of these - Question 2 - Select One
The radius of a circle is 7√π cm,then the area of the circle is .
A154cm2B49πcm2C22cm2D49cm2 - Question 3 - Select One
What is the ratio of the area of circle A to that of circle B ?
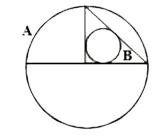 A12B14C2(√2+1)2D2(√2−1)2
A12B14C2(√2+1)2D2(√2−1)2
If the radius of a circle is tripled, the area becomes
View SolutionIf radius of circle C1 is 2 times the radius of circle C2, then ratio of area C1 to that of C2 is
View SolutionThe difference between the circumference and the radius of a circle is 37 cm. Find the area of the circle.
View SolutionIf the radius of a circle is increased by 8% ,then the area of the circle will be
View SolutionRadius of a circle is 2.23m. Area of the circle is
View Solution

