ΔDEF is similar to ΔGHI. The length of DE is 9 cm and length of the corresponding side GH is 16 cm. What is the ratio of areas of ΔDEF:ΔGHI ?
3:4
9:16
81:256
16:9
The correct Answer is:C
To find the ratio of the areas of triangle DEF to triangle GHI, we can follow these steps:
Step 1: Understand the relationship between similar triangles
Since triangle DEF is similar to triangle GHI, the ratio of their areas is equal to the square of the ratio of their corresponding sides.
Step 2: Identify the lengths of the corresponding sides
We are given:
- Length of side DE = 9 cm
- Length of corresponding side GH = 16 cm
Step 3: Calculate the ratio of the corresponding sides
The ratio of the lengths of the sides DE to GH is:
Ratio of sides=DEGH=9 cm16 cm=916
Step 4: Calculate the ratio of the areas
The ratio of the areas of the triangles is the square of the ratio of the corresponding sides:
Ratio of areas=(DEGH)2=(916)2
Step 5: Perform the squaring operation
Calculating the square of the ratio:
(916)2=92162=81256
Step 6: Write the final answer
Thus, the ratio of the areas of triangle DEF to triangle GHI is:
Area Ratio=81:256
---
Since triangle DEF is similar to triangle GHI, the ratio of their areas is equal to the square of the ratio of their corresponding sides.
We are given:
- Length of side DE = 9 cm
- Length of corresponding side GH = 16 cm
The ratio of the lengths of the sides DE to GH is:
Ratio of sides=DEGH=9 cm16 cm=916
The ratio of the areas of the triangles is the square of the ratio of the corresponding sides:
Ratio of areas=(DEGH)2=(916)2
Calculating the square of the ratio:
(916)2=92162=81256
Thus, the ratio of the areas of triangle DEF to triangle GHI is:
Area Ratio=81:256
Topper's Solved these Questions
- BOOK - KIRAN PUBLICATIONCHAPTER - MENSURATIONEXERCISE - TYPE - III21videos
MENSURATION
- BOOK - KIRAN PUBLICATIONCHAPTER - MENSURATIONEXERCISE - TYPE - IV169videos
MENSURATION
- BOOK - KIRAN PUBLICATIONCHAPTER - MENSURATIONEXERCISE - Test Yourself28videos
MENSURATION
- BOOK - KIRAN PUBLICATIONCHAPTER - LCM AND HCF EXERCISE - Test Yourself18videos
LCM AND HCF
- BOOK - KIRAN PUBLICATIONCHAPTER - MISCELLANEOUSEXERCISE - TYPE-VI15videos
MISCELLANEOUS
Similar Questions
Knowledge Check
- Question 1 - Select One
ΔABC is similar to ΔPQR. Length of AB is 16 cm and length of the corresponding side PQ is 9 cm. If area of ΔABC is 1024 sq. cm, what is the area of ΔPQR?
A768 sq. cmB32 sq. cmC324 sq. cmD128 sq. cm - Question 2 - Select One
ΔABC is similar to ΔDEF. The ratio of their perimeters is 4 :1 The ratio of their areas is
A4:1B16:1C8:1D8√2:1 - Question 3 - Select One
ΔABC is similar to ΔDEF. If the ratio of similar sides is k:1, the ratio of their areas is
Ak2:1B2k:1Ck22:1D2k2:1
In ΔABC,D,E,F are respectively the mid points of the sides AB, BC and AC. Find ratio of the area of ΔDEF and area of ΔABC.
View SolutionIf the ratio of areas of two similar triangles is 9:16 then the ratio of their corresponding sides is
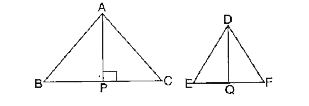
View SolutionTriangles ABC and DEF are similar. If the length of the perpendicular AP from A on the opposite side BC is 2 cm and the length of the perpendicular DQ from D on the opposite side EF is 1 cm, then what is the area of ΔABC?
 View Solution
View SolutionIf ΔABC is similar to ΔDEF such that BC = 3 cm, EF = 4 cm and area of ΔABC=54cm2, then the area of ΔDEF is :
View SolutionThe length of the sides of a triangle are in the ratio 3:4:5 and its perimeter is 144 cm. The area of the triangle is
View Solution