A sphere and a hemisphere have the same volume. The ratio of their curved surface area is :
2−32:1
223:1
4−23:1
213:1
The correct Answer is:D
To solve the problem of finding the ratio of the curved surface areas of a sphere and a hemisphere that have the same volume, we can follow these steps:
1. Define the Radii:
Let the radius of the sphere be R and the radius of the hemisphere also be R.
2. Volume of the Sphere:
The volume Vs of a sphere is given by the formula:
Vs=43πR3
3. Volume of the Hemisphere:
The volume Vh of a hemisphere is given by the formula:
Vh=23πR3
4. Set Volumes Equal:
Since the volumes of the sphere and hemisphere are equal, we can set the two equations equal to each other:
43πR3=23πr3
5. Cancel Common Terms:
We can cancel 23π from both sides:
2R3=r3
6. Solve for r:
Taking the cube root of both sides gives:
r=R(12)1/3
7. Curved Surface Area of the Sphere:
The curved surface area As of the sphere is given by:
As=4πR2
8. Curved Surface Area of the Hemisphere:
The curved surface area Ah of the hemisphere is given by:
Ah=2πr2
9. Substituting r:
Substitute r from step 6 into the hemisphere's surface area formula:
Ah=2π(R(12)1/3)2=2πR2(12)2/3
10. Calculate the Ratio:
Now, we can find the ratio of the curved surface areas:
Ratio=AsAh=4πR22πR2(12)2/3=42(12)2/3=42⋅(22/3)=2⋅22/3
11. Final Simplification:
The ratio simplifies to:
Ratio=21+2/3=25/3
Final Answer:
The ratio of the curved surface area of the sphere to the curved surface area of the hemisphere is 25/3.
Let the radius of the sphere be R and the radius of the hemisphere also be R.
The volume Vs of a sphere is given by the formula:
Vs=43πR3
The volume Vh of a hemisphere is given by the formula:
Vh=23πR3
Since the volumes of the sphere and hemisphere are equal, we can set the two equations equal to each other:
43πR3=23πr3
We can cancel 23π from both sides:
2R3=r3
Taking the cube root of both sides gives:
r=R(12)1/3
The curved surface area As of the sphere is given by:
As=4πR2
The curved surface area Ah of the hemisphere is given by:
Ah=2πr2
Substitute r from step 6 into the hemisphere's surface area formula:
Ah=2π(R(12)1/3)2=2πR2(12)2/3
Now, we can find the ratio of the curved surface areas:
Ratio=AsAh=4πR22πR2(12)2/3=42(12)2/3=42⋅(22/3)=2⋅22/3
The ratio simplifies to:
Ratio=21+2/3=25/3
The ratio of the curved surface area of the sphere to the curved surface area of the hemisphere is 25/3.
Topper's Solved these Questions
- MENSURATIONBook:KIRAN PUBLICATIONChapter:MENSURATIONExercise:TYPE - V
Explore 304 Videos
- MENSURATIONBook:KIRAN PUBLICATIONChapter:MENSURATIONExercise:TYPE VI
Explore 47 Videos
- MENSURATIONBook:KIRAN PUBLICATIONChapter:MENSURATIONExercise:TYPE - III
Explore 21 Videos
- LCM AND HCF Book:KIRAN PUBLICATIONChapter:LCM AND HCF Exercise:Test Yourself
Explore 18 Videos
- MISCELLANEOUSBook:KIRAN PUBLICATIONChapter:MISCELLANEOUSExercise:TYPE-VI
Explore 15 Videos
Similar Questions
A sphere and the base of a cylinder have equal radii. The diameter of the sphere is equal to the height of the cylinder. The ratio of the curved surface are of the cylinder and surface area of the sphere is __________.
View SolutionAs shown in the adjacent figure, a sphere is placed in a cylinder. It touches the top, bottom and the curved surface of the cylinder. If radius of the base of the cylinder is 'r',
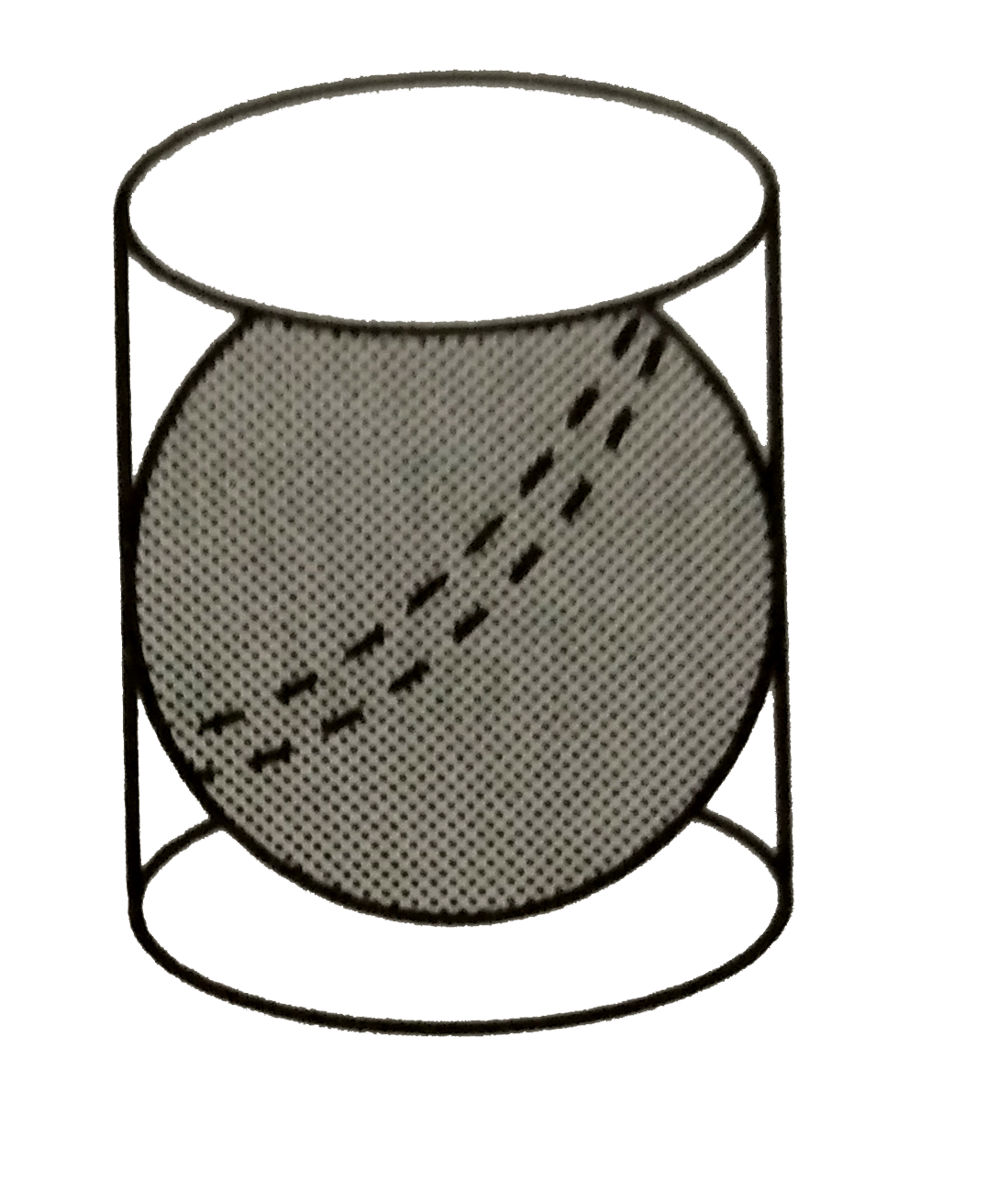
(i) what is ratio of the radii of the sphere and the cylinder?
(ii)what is the ratio of the curved surface area of the cylinder and the surface area of the sphere?
(iii) what is the ratio of the volumes of the cylinder and the sphere?
View Solution
Knowledge Check
A sphere and a hemisphere have the same volume. The ratio of their radii is
A1:2B1:8C1:√2D1:3√2A sphere and a hemisphere have the same surface area. The ratio of their volumes is
A√34:1B3√34:1C√38:1D3√38:1A sphere and a hemisphere have the same radius. Then the ratio of their respective total surface areas is
A2:1B1:2C4:3D3:4
If the ratio of the radii of a sphhere and a hemisphere is 3:5 then the ratio of its curved surface area is
View SolutionA parallelopiped whose sides are in ratio 2:4:8 have the same volume as a cube. The ratio of their surface area is :
View SolutionA sphere and a cylinder have equal volume and equal radius. The ratio of the curved surface area of the cylinder to that of the sphere is
View SolutionA solid right circular cylinder and a solid hemisphere stand on equal bases and have the same height. The ratio of their whole surface area is :
View SolutionThe volume of two sphere are in the ratio 8:27. The ratio of their surface area is :
View Solution