From a right circular cylinder of radius 10 cm and height 21 cm, a right circular cone of same base radius is removed. If the volume of the remaining portion is 4400cm3, then the height of the removed cone (taking π=227) is :
15 cm
18 cm
21 cm
24 cm
The correct Answer is:C
To find the height of the removed cone from the right circular cylinder, we can follow these steps:
Step 1: Calculate the volume of the cylinder
The volume V of a cylinder is given by the formula:
V=πr2h
where r is the radius and h is the height.
Given:
- Radius of the cylinder r=10 cm
- Height of the cylinder H=21 cm
Substituting these values into the formula:
Vcylinder=π(10)2(21)=π×100×21=2100πcm3
Using π=227:
Vcylinder=2100×227=6600cm3
Step 2: Set up the equation for the remaining volume
The volume of the remaining portion after removing the cone is given as 4400cm3. Therefore, we can write:
Vremaining=Vcylinder−Vcone
Substituting the known values:
4400=6600−Vcone
Step 3: Calculate the volume of the cone
Rearranging the equation gives:
Vcone=6600−4400=2200cm3
The volume V of a cone is given by the formula:
V=13πr2h
where r is the radius and h is the height of the cone.
Using the same radius r=10 cm for the cone, we can substitute:
2200=13π(10)2h
2200=13π×100×h
2200=100πh3
Step 4: Substitute the value of π and solve for h
Substituting π=227:
2200=100×227×h3
Multiplying both sides by 3:
6600=2200h7
Multiplying both sides by 7:
46200=2200h
Dividing both sides by 2200:
h=462002200=21cm
Final Answer
The height of the removed cone is 21cm.
---
The volume V of a cylinder is given by the formula:
V=πr2h
where r is the radius and h is the height.
- Radius of the cylinder r=10 cm
- Height of the cylinder H=21 cm
Vcylinder=π(10)2(21)=π×100×21=2100πcm3
Vcylinder=2100×227=6600cm3
The volume of the remaining portion after removing the cone is given as 4400cm3. Therefore, we can write:
Vremaining=Vcylinder−Vcone
Substituting the known values:
4400=6600−Vcone
Rearranging the equation gives:
Vcone=6600−4400=2200cm3
V=13πr2h
where r is the radius and h is the height of the cone.
2200=13π(10)2h
2200=13π×100×h
2200=100πh3
Substituting π=227:
2200=100×227×h3
Multiplying both sides by 3:
6600=2200h7
Multiplying both sides by 7:
46200=2200h
Dividing both sides by 2200:
h=462002200=21cm
The height of the removed cone is 21cm.
Topper's Solved these Questions
- MENSURATIONBOOK - KIRAN PUBLICATIONCHAPTER - MENSURATIONEXERCISE - TYPE VI
47 Videos
- MENSURATIONBOOK - KIRAN PUBLICATIONCHAPTER - MENSURATIONEXERCISE - TYPE VII
60 Videos
- MENSURATIONBOOK - KIRAN PUBLICATIONCHAPTER - MENSURATIONEXERCISE - TYPE - IV
169 Videos
- LCM AND HCF BOOK - KIRAN PUBLICATIONCHAPTER - LCM AND HCF EXERCISE - Test Yourself
18 Videos
- MISCELLANEOUSBOOK - KIRAN PUBLICATIONCHAPTER - MISCELLANEOUSEXERCISE - TYPE-VI
15 Videos
Similar Questions
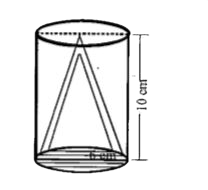
From a right circular cylinder with height 10cm and radius of base 6cm, a right circular cone of the same height and base is removed. Find the volume of the remaining solid.
View SolutionFrom a solid right circular cylinder with height 10 cm and radius of the base 6 cm, a right circular cone of the the same height and same base is removed . find the volume of the remaining solid
View Solution
Knowledge Check
Volume of a right circular cylinder of height 21 cm and base radius 5 cm is
A1255 cm2B1050 cm2C1175 cm2D1650 cm2Volume of a right circular cylinder of height 21 cm and base radius 5 cm is :
A1255cm3B1050cm3C1175cm3D1650cm3From a solid cylinder of height 10 cm and radius of the base 6 cm, a cone of same height and same base is removed. The volume of the remaining solid is :
A240π cu. cmB5280 cu. cmC620π cu. cmD360π cu. cm
From a solid right circular cylinder with height 10 cm and radius of the base 6 cm, a right circular cone of the same height and base is removed. Find the volume of the remaining solid. (Take π=3.14)
View SolutionThe height of a right circular cone is 7 cm and radius is 24 cm. Find the slant height of the cone.
View SolutionA metallic sphere of radius 7 cm is melted and recast in to right circular cone of same radius. Find the height of the cone.
View SolutionThe radius and slant height of a right circular cone are 5 cm and 13 cm respectively. What is the volume of the cone ?
View SolutionFrom a solid circular cylinder with height 10 cm and radius of the base 6 cm, a circular cone of the same height and same base is removed. Find the volume of remaining solid and also find the whole surface area.
View Solution