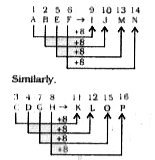
ABEF : IJMN : : CDGH : ?
JKNP
KLNQ
JKMN
KLOP
The correct Answer is:D
Topper's Solved these Questions
- ANALOGY OR SIMILARITY BOOK - KIRAN PUBLICATIONCHAPTER - ANALOGY OR SIMILARITY EXERCISE - TYPE-V
37 Videos
- ANALOGY OR SIMILARITY BOOK - KIRAN PUBLICATIONCHAPTER - ANALOGY OR SIMILARITY EXERCISE - TYPE-IV
198 Videos
- ARRANGEMENT OF WORDS IN LOGICAL ORDER BOOK - KIRAN PUBLICATIONCHAPTER - ARRANGEMENT OF WORDS IN LOGICAL ORDER EXERCISE - TYPE II
199 Videos
Similar Questions
Parallelogram ABCD and rectangle ABEF have the same base AB and also have equal areas. Show that the perimeter of the parallelogram is greater than that of the rectangle. GIVE : AgmABCD and a rectangle ABEF with the same base AB and equal areas. TO PROVE : Perimeter of ^(gm)ABCD>Perimeteroectan≥l ABEF i.e. AB+BC+CD+AD>AB+BE+EF+AF
View SolutionIf in a certain code language ‘BHAI’ is written as ‘2819’, then how will ‘CDGH’ be written in that language?
एक कोड भाषा में, BHAI’ को ‘2819’ लिखा जाता है| ‘CDGH’ को उस भाषा में कैसे लिखा जाएगा?
View Solution
Knowledge Check
A series is given, with one term missing. Choose the correct alternative from the given ones.
ABEF, IJMN, ?AQRVUBQRUVCQRVWDQSVUABCD is a trapezium in which AB is parallel to DC, AD = BC, AB = 6 cm, AB = EF and DF = EC. If two lines AF and BE are drawn so that area of ABEF is half of ABCD. Find DF/CD
 A25B13C25D14
A25B13C25D14Direct Alphabetic Sequential Relationship CD:GH:: LM:?
ADCBEGCABDJJ
Parallelogram ABCD and rectangle ABEF are on the same base AB and have equalareas. Show that the perimeter of the parallelogram is greater than that of the rectangle.
View SolutionThe following figure shows two paralelograms ABCD and ABEF prove that
area of ΔADF=areaofΔBCE
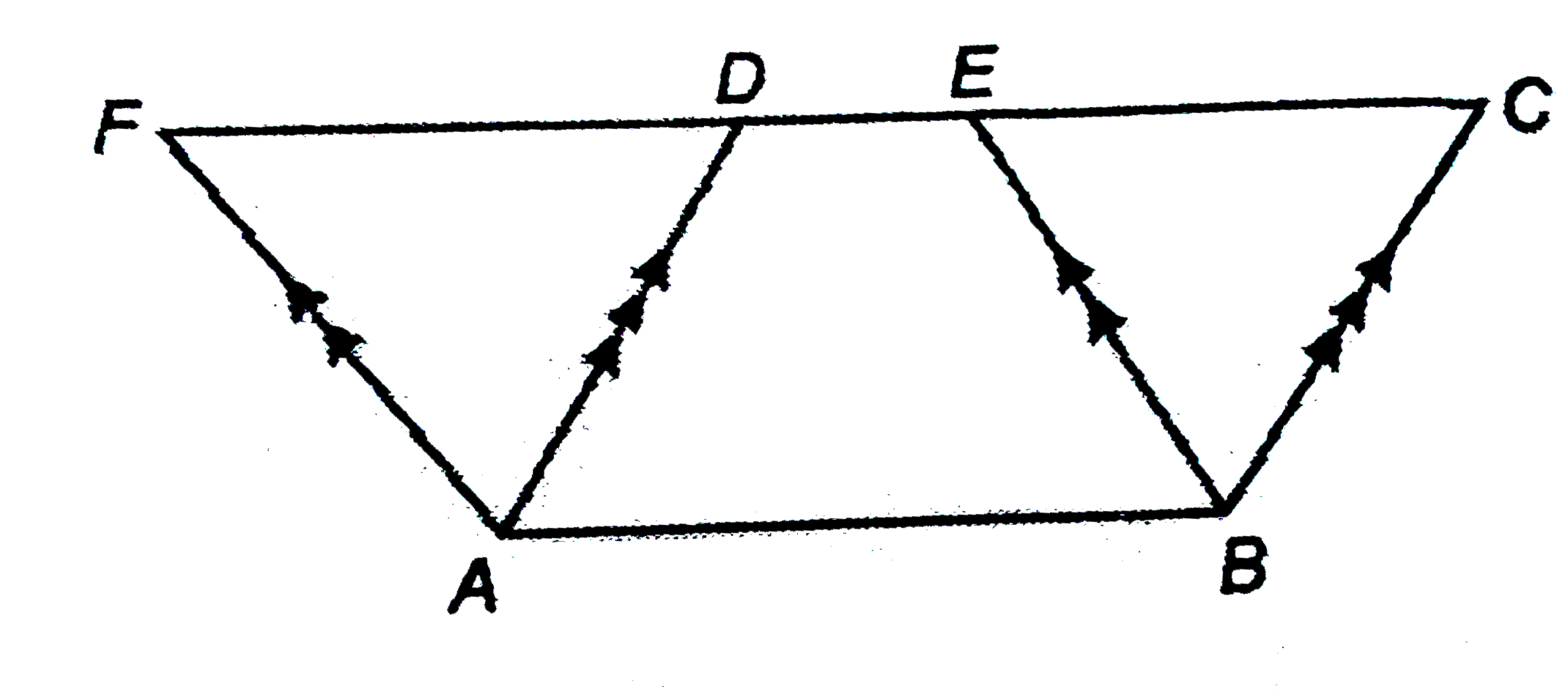
View SolutionParallelogram ABCD and rectangle ABEF are on the same base AB and have equal areas. Show that the perimeter of the parallelogram is greater than that of the rectangle.
View SolutionABCD is a trapezium in which AD||BC, AB = 9 cm BC = 12 cm CD = 15 cm DA = 30 cm find the sum of diagonals's square
View SolutionIn the given figure, ABCD and ABEF aretwo cyclic quadrilaterals. If ∠BCD=110∘ then ∠BEF=?

View Solution