EAC : KGI :: HDF : ?
PLN
KIJ
FBD
NJL
The correct Answer is:D
Topper's Solved these Questions
- ANALOGY OR SIMILARITY BOOK - KIRAN PUBLICATIONCHAPTER - ANALOGY OR SIMILARITY EXERCISE - TYPE-IV (Select the related letter from the given alternatives.)
230 Videos
- ANALOGY OR SIMILARITY BOOK - KIRAN PUBLICATIONCHAPTER - ANALOGY OR SIMILARITY EXERCISE - TYPE-V
37 Videos
- ANALOGY OR SIMILARITY BOOK - KIRAN PUBLICATIONCHAPTER - ANALOGY OR SIMILARITY EXERCISE - TYPE-III
373 Videos
- ARRANGEMENT OF WORDS IN LOGICAL ORDER BOOK - KIRAN PUBLICATIONCHAPTER - ARRANGEMENT OF WORDS IN LOGICAL ORDER EXERCISE - TYPE II
199 Videos
Similar Questions
Let D and E be two points on the side BC of △ABC such that AD = AE and ∠BAD=∠EAC. If AB = (3x+1)cm , BD = 9cm , AC = 34cm and EC = (y + 1) cm, then the value of (x + y) is:
△ABC में, D और E भुजा BC पर दो बिंदु इस प्रकार है की AD = AE और ∠BAD=∠EAC । यदि AB = (3x +1) cm, BD = 9cm, AC = 34cm और EC = (y+1) cm है, तो (x + y) का मान है
View SolutionPoint D,E are taken on the side BC of an acute angled triangle ABC,, such that BD=DE=EC. If ∠BAD=x,∠DAE=yand∠EAC=z then the value of sin(x+y)sin(y+z)sinxsinz is ______
View Solution
Knowledge Check
In the following questions, a series is given, with one term missing. Choose the correct alternative from the given ones that will complete the series.
EAC, GCE, IEG, ?AJHIBKGICJGIDKIJIn ΔABC,∠C=54∘, the perpendicular bisector of AB at D meets BC at E. If ∠EAC=42∘, then what is the value (in degrees) of ∠ABC?
A25B42C50D60In ΔABCBC⊥AC at D.E is a point on BC such that ∠BEA=x∘ If ∠EAC=36∘and∠EBD=40∘, then the value of x is:
A68∘B86∘C72∘D78∘
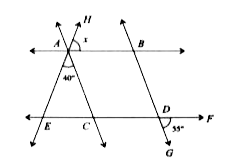
In the given figure AB is parallel to CD and AC is parallel to BD. If ∠EAC=40∘,∠FDG=55∘,∠HAB=x∘, then what is the value of x ?
View SolutionIn the given figure , C is the midpoint of AB, if ∠DCA=∠ECBand∠DBC=∠EAC , Prove that DC=EC and BD=AE
View SolutionIn the given figure, squares ABDE and AFGC are drawn on the side AB and the hypotenuse AC of the right angle triangle ABC. If BH is perpendicular to FG, Prove that
(i) ΔEAC≅ΔBAF
(ii) area of square ABDE= area of rectangle ARHF.

View SolutionArrange the following in decreasing order as directed.
(a) Decreasing order of EN:H,O,Al,F
b. Decreasing order of radii: Ar,Br,Ca2+,Mg2+
c. Decreasing order of EA:C,N,Be,F,O,CI
d. Decreasing order of IE and EA:F,Cl,Br,I
e Decreasing order of EN:F,N,O,Cl,S
f. Decreasing order of IE:Ne,O,Na,Na⊕
g. Decreasing electropositive character: Na,Cu,Zn
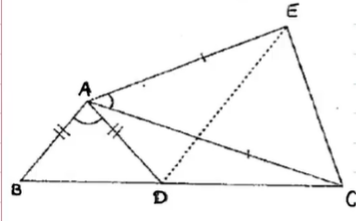
View SolutionIn Figure, AC=AE, AB=AD and ∠BAD=∠EAC. Prove that BC=DE
View Solution

