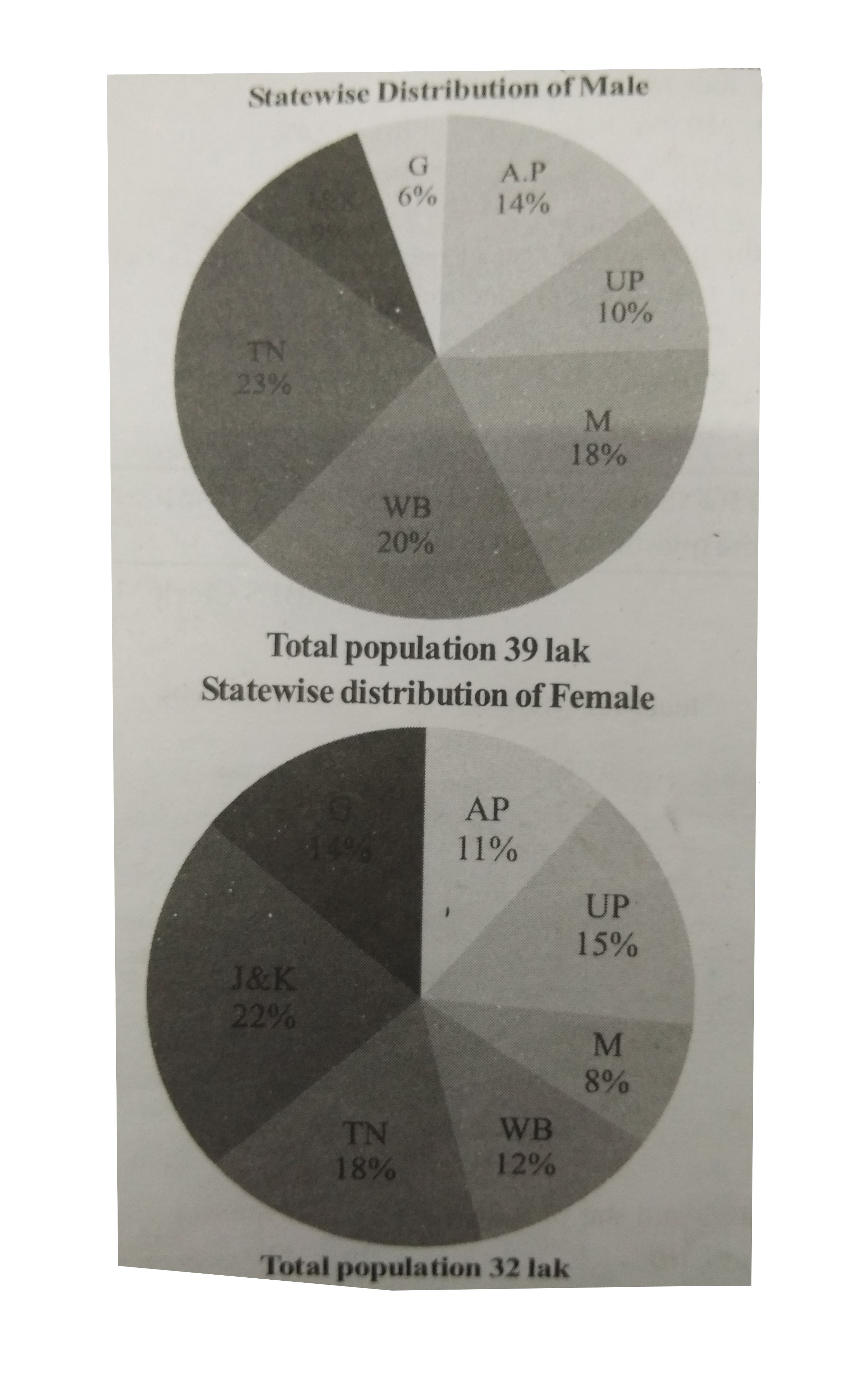
What is the population of state A?
I. After an increase in the population of state A by it becomes lakhs.
II. Ratio of population of state A to that of state B is .
A) only I is sufficient
B) Both are required
C) only II is sufficient
D) None of these
The correct Answer is:Population of state
lakhs
To determine the population of state A, we need to analyze the two statements provided:
Step 1: Analyze Statement I
Statement I states that after an increase in the population of state A by 12%, it becomes 627.20 lakhs.
This means that 112% of the original population (which includes the 12% increase) is 627.20 lakhs.
To find the original population (100%), we can set up the equation:
112% of population=627.20 lakhs
This can be expressed mathematically as:
112100×Population=627.20
Step 2: Solve for the Original Population
To find the original population, we rearrange the equation:
Population=627.20×100112
Calculating this gives:
Population=62720112=560 lakhs
Step 3: Analyze Statement II
Statement II states that the ratio of the population of state A to that of state B is 4:5.
While this provides a relationship between the populations of states A and B, it does not give us enough information to determine the exact population of state A on its own. Without knowing the population of state B or any additional information, we cannot find the population of state A.
Conclusion
From the analysis:
- Statement I alone is sufficient to determine the population of state A (560 lakhs).
- Statement II alone is not sufficient to determine the population of state A.
Thus, the answer is that only Statement I is needed to find the population of state A.
Final Answer
The population of state A is 560 lakhs.
---
Statement I states that after an increase in the population of state A by 12%, it becomes 627.20 lakhs.
112% of population=627.20 lakhs
This can be expressed mathematically as:
112100×Population=627.20
To find the original population, we rearrange the equation:
Population=627.20×100112
Population=62720112=560 lakhs
Statement II states that the ratio of the population of state A to that of state B is 4:5.
From the analysis:
- Statement I alone is sufficient to determine the population of state A (560 lakhs).
- Statement II alone is not sufficient to determine the population of state A.
The population of state A is 560 lakhs.
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
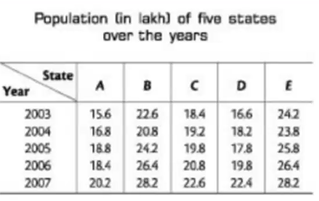
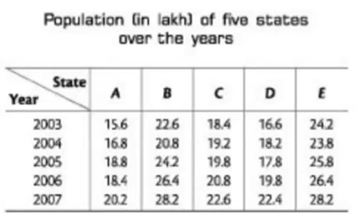
What is the ratio of the population of state A in 2003 to the population of stateE in 2007?
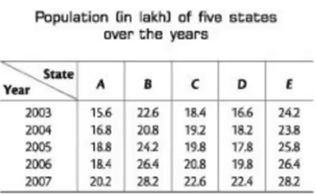 A37:22B22:37C47:26D26:47
A37:22B22:37C47:26D26:47 - Question 2 - Select One
What is the population of state A in year1999?
I. The population of state A is 1,20,000 in 1997 and it increases 20% every year
II. Population of state A is double the population of state B in 1997AIf the Statement I alone is sufficient to answer the question but the statement I alone is not sufficientBIf the Statement II alone is sufficient to answer the question but the statement alone is not sufficientCIf both Statements I and II together are needed to answer the questionDIf either the statement I alone or Statement II alone is sufficient to answer the question - Question 3 - Select One
In each of the following questions there is a question which is followed by three statements. Read the question and all the three statements and then decide which of the statement(s) is/are sufficient to answer the question
What is the population of the state ’A’?
After the increases of 15% the population of ‘A’ increases 1⋅61 lakh
The ratio in the population of the States ’A’ and ‘B’ is 7:8
The population of the State ‘B’ is 1⋅6lakhAOnly 1BOnly 2 and 3COnly 1 and 3DEither 1 or 2 and 3
Population of state E in 2004 is approximately what per cent of the population of state D in 2006?
 View Solution
View SolutionWhat is the total population of all the states together (in lakh) in 2005?
View SolutionPopulation of state E in 2007 is what per cent of the total population of all the states together in that year?
 View Solution
View SolutionWhich is the higest populated state of India ?
View SolutionMarxist philosophy of population dynamics states that
View Solution