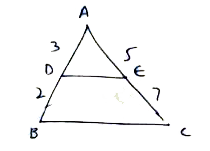
ABC is a triangle median CD and BE intersects at point O then find the ratio of area (ΔODE):(ΔABC).
1:6
6:1
1:12
12:1
The correct Answer is:C
Step by step video, text & image solution for ABC is a triangle median CD and BE intersects at point O then find the ratio of area (DeltaODE) : (DeltaABC). by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CENTRE OF TRIANGLEBOOK - LUCENT PUBLICATIONCHAPTER - CENTRE OF TRIANGLEEXERCISE - EXERCISE-6B
8 Videos
- CENTRE OF TRIANGLEBOOK - LUCENT PUBLICATIONCHAPTER - CENTRE OF TRIANGLEEXERCISE - EXERCISE-6B
8 Videos
- ALGEBRAIC IDENTITIES BOOK - LUCENT PUBLICATIONCHAPTER - ALGEBRAIC IDENTITIES EXERCISE - Exercise - 1B
28 Videos
- CIRCLE AND ITS TANGENT LINESBOOK - LUCENT PUBLICATIONCHAPTER - CIRCLE AND ITS TANGENT LINESEXERCISE - EXERCISE 8B
27 Videos
Similar Questions
Knowledge Check
AB and CD are parallel sides of a trapezium ABCD. Its diagonals intersect at point O. If the ratio of areas of ΔAOB and ΔCOD is 81:16, then the ratio of parallel sides AB : CD is
A3:1B2:1C3:2D9:4ABC is a triangle median CD and BE intersects at point O then find the ratio of area (ΔODE):(ΔABC).
A12:1B4:3C3:4D1:12
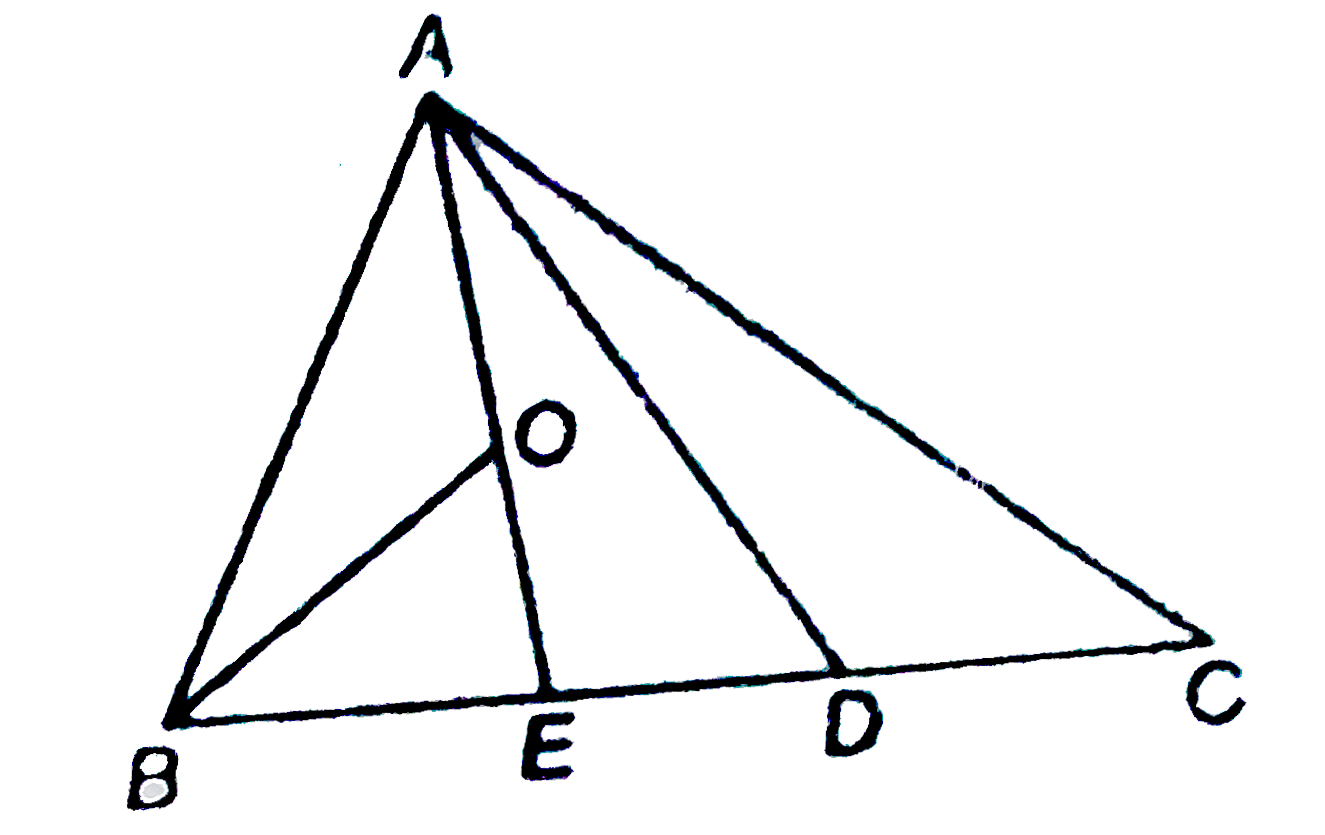
In a ΔABC,∠B=90∘, median AD and CF intersects at 'O' . Find the ratio of area of ΔAOCandBDOF.
View SolutionIn a ΔABC,∠B=90∘, median AD and CF intersects at 'O' . Find the ratio of area of ΔAOCandBDOF.
View SolutionIn the given figure, D is the mid-point of BC, E is the mid-point of BD and O is the mid-point of AE. Find the ratio of area of ΔBOEandΔABC
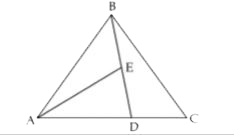
View SolutionIn the given figure ABC is a triangle in which 3AD = CD and E lies on BD, DE = 2BE. What is the ratio of area of ΔABC and area of ΔABE?
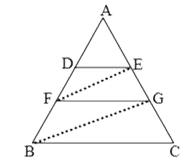
View SolutionIn a ΔABC,DE||EG||BCandEF∣∣BG and D is a midpoint of AF. Find the ratio of area of ΔDEF:ΔABC
View SolutionIn ΔABC,DandE are the midpoint of AB and AC respectively. Find the ratio of the areas of ΔADEandΔABC.
View Solution