In a survey of 100 students, the number of students studying the various languages were found to be: English only 18, English but not Hindi 23, English and Sanskrit 8, English 26, Sanskrit 48, Sanskrit and Hindi 8, no language 24. Find:
How many students were studying English and Hindi?
The correct Answer is:=3
To solve the problem step by step, we will first organize the given information and then use it to find the number of students studying both English and Hindi.
Step 1: Organize the given data
We have the following information from the survey of 100 students:
- English only: 18
- English but not Hindi: 23
- English and Sanskrit: 8
- Total studying English: 26
- Total studying Sanskrit: 48
- Sanskrit and Hindi: 8
- No language: 24
Step 2: Define the variables
Let:
- A = Students studying only English
- B = Students studying English and Hindi
- C = Students studying only Hindi
- D = Students studying English and Sanskrit
- E = Students studying only Sanskrit
- F = Students studying Sanskrit and Hindi
- G = Students studying only Hindi
- H = Students studying no language
Step 3: Set up equations based on the information
From the information provided, we can set up the following equations:
1. A = 18 (English only)
2. A + D = 23 (English but not Hindi)
3. D + B = 8 (English and Sanskrit)
4. A + B + D = 26 (Total studying English)
5. E + F = 48 (Total studying Sanskrit)
6. H = 24 (No language)
Step 4: Calculate the values
From equation 1, we know A = 18.
From equation 2:
- A + D = 23
- 18 + D = 23
- D = 23 - 18 = 5
From equation 4:
- A + B + D = 26
- 18 + B + 5 = 26
- B = 26 - 18 - 5 = 3
Step 5: Conclusion
The number of students studying both English and Hindi (B) is 3.
Final Answer
Thus, the number of students studying English and Hindi is 3.
We have the following information from the survey of 100 students:
- English only: 18
- English but not Hindi: 23
- English and Sanskrit: 8
- Total studying English: 26
- Total studying Sanskrit: 48
- Sanskrit and Hindi: 8
- No language: 24
Let:
- A = Students studying only English
- B = Students studying English and Hindi
- C = Students studying only Hindi
- D = Students studying English and Sanskrit
- E = Students studying only Sanskrit
- F = Students studying Sanskrit and Hindi
- G = Students studying only Hindi
- H = Students studying no language
From the information provided, we can set up the following equations:
1. A = 18 (English only)
2. A + D = 23 (English but not Hindi)
3. D + B = 8 (English and Sanskrit)
4. A + B + D = 26 (Total studying English)
5. E + F = 48 (Total studying Sanskrit)
6. H = 24 (No language)
From equation 1, we know A = 18.
- A + D = 23
- 18 + D = 23
- D = 23 - 18 = 5
- A + B + D = 26
- 18 + B + 5 = 26
- B = 26 - 18 - 5 = 3
The number of students studying both English and Hindi (B) is 3.
Thus, the number of students studying English and Hindi is 3.
Topper's Solved these Questions
- BOOK - DISHA PUBLICATIONCHAPTER - SET THEORYEXERCISE - Practice Exercises (Foundation Level)14videos
SET THEORY
- BOOK - DISHA PUBLICATIONCHAPTER - SET THEORYEXERCISE - Practice Exercises (Standard Level)31videos
SET THEORY
- BOOK - DISHA PUBLICATIONCHAPTER - RATIO,PROPORTION AND VARIATIONEXERCISE - Test Yourself15videos
RATIO,PROPORTION AND VARIATION
- BOOK - DISHA PUBLICATIONCHAPTER - TIME AND WORKEXERCISE - Test Yourself15videos
TIME AND WORK
Similar Questions
In a survey of 100 students, the number of students studying the various languages were found to be: English only 18, English but not Hindi 23, English and Sanskrit 8, English 26, Sanskrit 48, Sanskrit and Hindi 8, no language 24. Find:
How many students were studying Hindi?View SolutionIn a survey of 100 students, how many of students studying the various languages were found to study: English only 18, English but not Hindi 23, English and Sanskrit 8, English 26, Sanskrit 48, Sanskrit and Hindi 8, no language 24 Find:(i) how many students were studying Hindi (ii) how many students were studying English and Hindi
View Solution
Knowledge Check
- Question 1 - Select One
The Students of a class are offered three language (Hindi. English and French). 15 students learn all the three language whereas 28 students do not learn any language. The number of students learning Hindi and English but not French is twice the number of students learning Hindi and French but not English. The number of students learning English and French but not Hindi is thrice the number of students learning Hindi and French but not English. 23 students learn only Hindi and 17 students learn only English. The total number of students learning French is 46 and the total number of students learning only French is 11.
How many students learn English and French?A30B43C45D73 - Question 2 - Select One
The students of a class are offered three languages (Hindi, English and French). 15 students learn all the three languages whereas 28 students do not learn any language. The number of students learning Hindi and English but not French is twice the number of students learning Hindi French but not English. The number of students learning English and French but not Hindi is thrice the number of students learning Hindi and French but not English. 23 students learn only Hindi and 17 students learn only English. The total number of students learning French is 46 and the total number of students learning only French is 11.
How many students learn precisely two languages?A55B40C30D13 - Question 3 - Select One
The students of a class are offered three languages (Hindi, English and French). 15 students learn all the three languages whereas 28 students do not learn any language. The number of students learning Hindi and English but not French is twice the number of students learning Hindi French but not English. The number of students learning English and French but not Hindi is thrice the number of students learning Hindi and French but not English. 23 students learn only Hindi and 17 students learn only English. The total number of students learning French is 46 and the total number of students learning only French is 11.
How many students learn at least two languages?A15B30C45D55
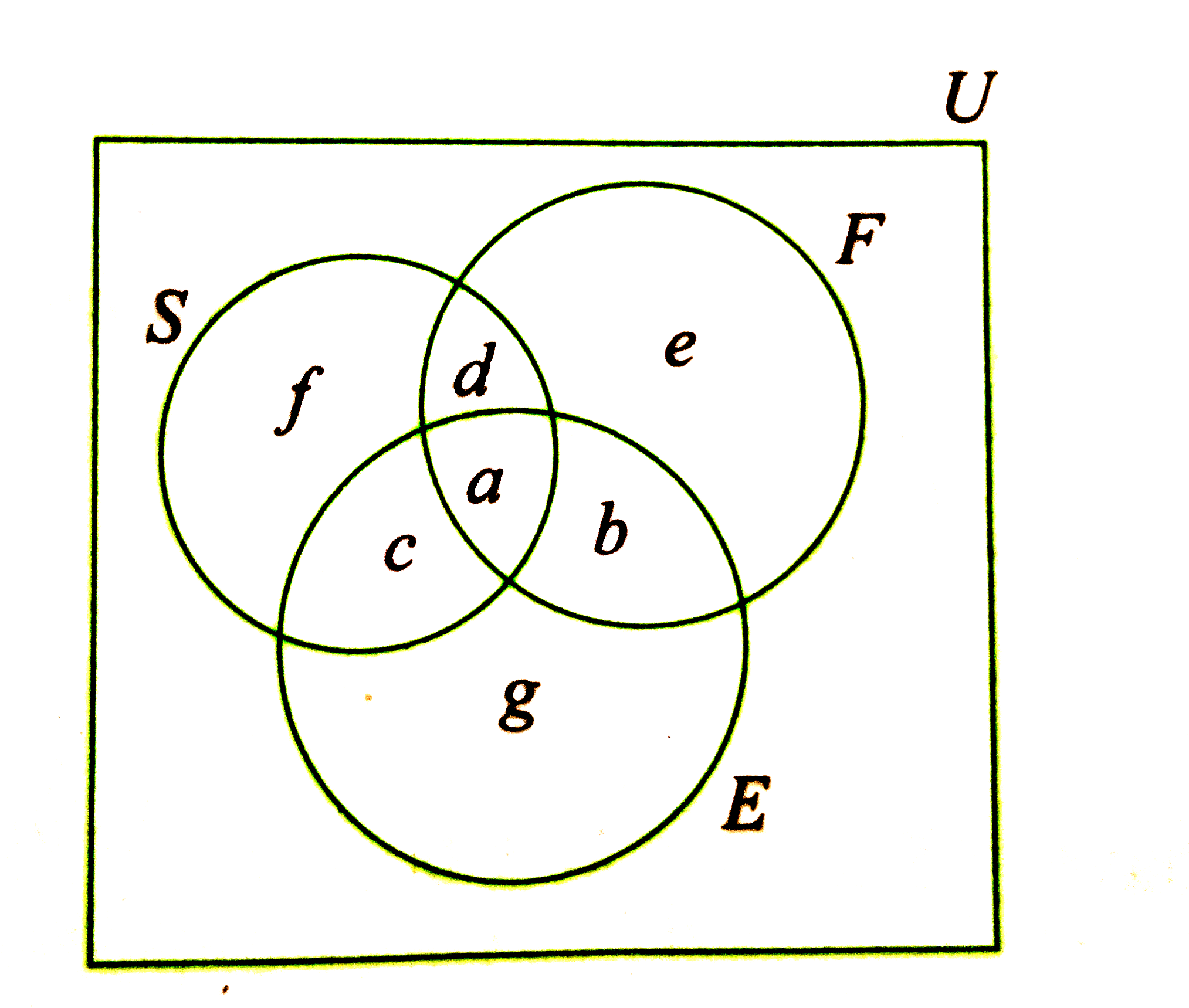
In a group of 50 students, the number of students studying French, English, Sanskrit were found to be as follows French = 17, English = 13, Sanskrit = 15 French and English = 09, English and Sanskrit = 4, French and Sanskrit = 5, English , French and Sanskrit = 3. Find the number of students who study
(i) only French, (ii) only English.
(iii) only Sanskrit. , (iv) English and Sanskrit but not French.
(v) French and Sanskrit but not English.
(vi) French and English but not Sanskrit.
(vii) atleast one of the three languages.
(viii) none of the three languages.View SolutionIn a group of 50 students, the number of students learning - French, English, Sanskrit were found to be as follows: French = 17, English = 13, Sanskrit = 15, French and English = 09, English and Sanskrit = 4, French and Sanskrit = 5, English, French and Sanskrit = 3. Find the number of students who are learning at?
French only
(ii) English only
(iii) Sanskrit only
(iv) English and Sanskrit but not French
(v) French and Sanskrit but not English
(vi) French and English but not Sanskrit
(vii) at least one of the three languages
(viii) none of the three languages
(ix) exactly one language (X) exactly two languages
 View Solution
View SolutionThe report of one survey of 100 students stated that the numbers studying the various languages were : Sanskrit, Hindi and Tamil, 5, Hindi and Sanskrit, 10, Tamil and Sanskrit, 8, Hindi and Tamil, 20, Sanskrit 30, Hindi 23, Tamil 50. The surveyor who prepared the report was fired. Why ?
View SolutionWhich response represents language, English, Hindi?
 View Solution
View SolutionThe students of a class are offered three languages (Hindi, English and French). 15 students learn all the three languages whereas 28 students do not learn any language. The number of students learning Hindi and English but not French is twice the number of students learning Hindi French but not English. The number of students learning English and French but not Hindi is thrice the number of students learning Hindi and French but not English. 23 students learn only Hindi and 17 students learn only English. The total number of students learning French is 46 and the total number of students learning only French is 11.
How many students learn at least one languages?View Solution

