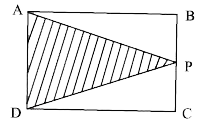
In ΔACD,AD=ACand∠C=2∠E. The distance between parallel lines AB and CD is h.

Then
I. Area of parallelogram ABCD
II. Area of ΔADE
I>II
I<II
I = II
Nothing can be said
The correct Answer is:C
Step by step video, text & image solution for In Delta ACD, AD = AC and angle C = 2 angle E. The distance between parallel lines AB and CD is h. Then I. Area of parallelogram ABCD II. Area of Delta ADE by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Updated on:21/07/2023Topper's Solved these Questions
- MENSURATIONBOOK - DISHA PUBLICATIONCHAPTER - MENSURATIONEXERCISE - Practice Exercises (EXPERT LEVEL)
45 Videos
- MENSURATIONBOOK - DISHA PUBLICATIONCHAPTER - MENSURATIONEXERCISE - TEST YOURSELF
15 Videos
- MENSURATIONBOOK - DISHA PUBLICATIONCHAPTER - MENSURATIONEXERCISE - Practice Exercises ( Foundation Level)
70 Videos
- LOGARITHMSBOOK - DISHA PUBLICATIONCHAPTER - LOGARITHMSEXERCISE - Test Yourself
15 Videos
- MOCK TEST - 3BOOK - DISHA PUBLICATIONCHAPTER - MOCK TEST - 3EXERCISE - Multiple Choice Questions
20 Videos
Similar Questions
Knowledge Check
In a ΔABC,∠A:∠B:∠C=2:3:4 A line CD drawn parallel to AB, then ∠ACD is
A80∘B20∘C40∘D60∘The area of a parallelogram ABCD is equal to that right angled isosceles triangle whose hypotenuse is l cm. If O is a point inside the parallelogram ABCD then sum of areas of ΔAOBandΔCOD is.
Al22cm2Bl24cm2Cl28cm2Dl216cm2
In a ΔABC,∠B=2∠C Angle bisector AD and BE intersect of O. AB = CD find ∠ABC
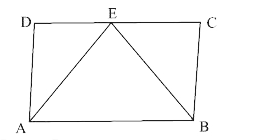
View SolutionIn given figure. If area of parallelogram ABCD is 30cm2 then find ar (ΔADE)+ ar (ΔBCE)
View SolutionFind the ratio of AD and CD when AB = 3 cm BC = 4 cm ∠B=90∘. Also find area of ΔADB
View SolutionO' is any point on diagonal AC of a parallelogram ABCD. Prove that :
area of ΔAOD= area of ΔAOB
View SolutionPerpendicular distance between point & line || Distance between two parallel line || Image OF a point with respect to various cases || Area OF parallelogram & Isosceles triangle
View SolutionABCD and BCFE are parallelgorams. If area of triangle EBC=480cm2,AB=30cmandBC=40cm. Calculate
(i) area of parallelogram ABCD
(ii) area of parallelogram BCEF
(iii) length of altitude from A on CD.
(iv) area of ΔECF
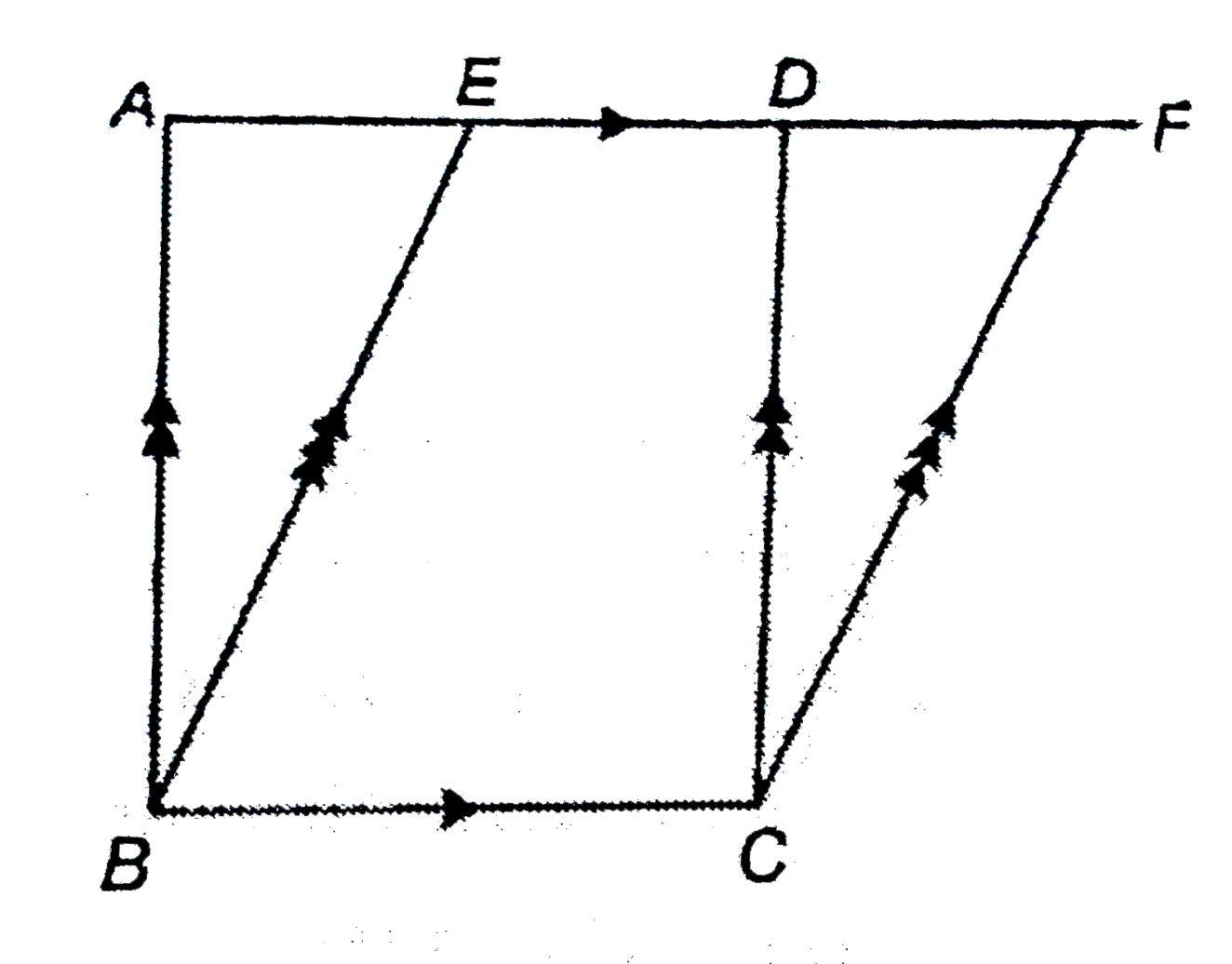
View Solution