A charge particle q is projected in a uniform magnetic field of flux density B at an angle θ with the direction of flux density. Write down the expression of magnetic force acting on the charge particle in vector form.
Expression of magnetic force acting on the charge particle in vector from is given by
F=q(v×B)=q|v||B|sinθ
Similar Questions
A charged particle (q,m) enters perpendicular in a uniform magnetic field B and comes out field as shown. Find the angle of deviation θ for particle to cross magnetic field will be
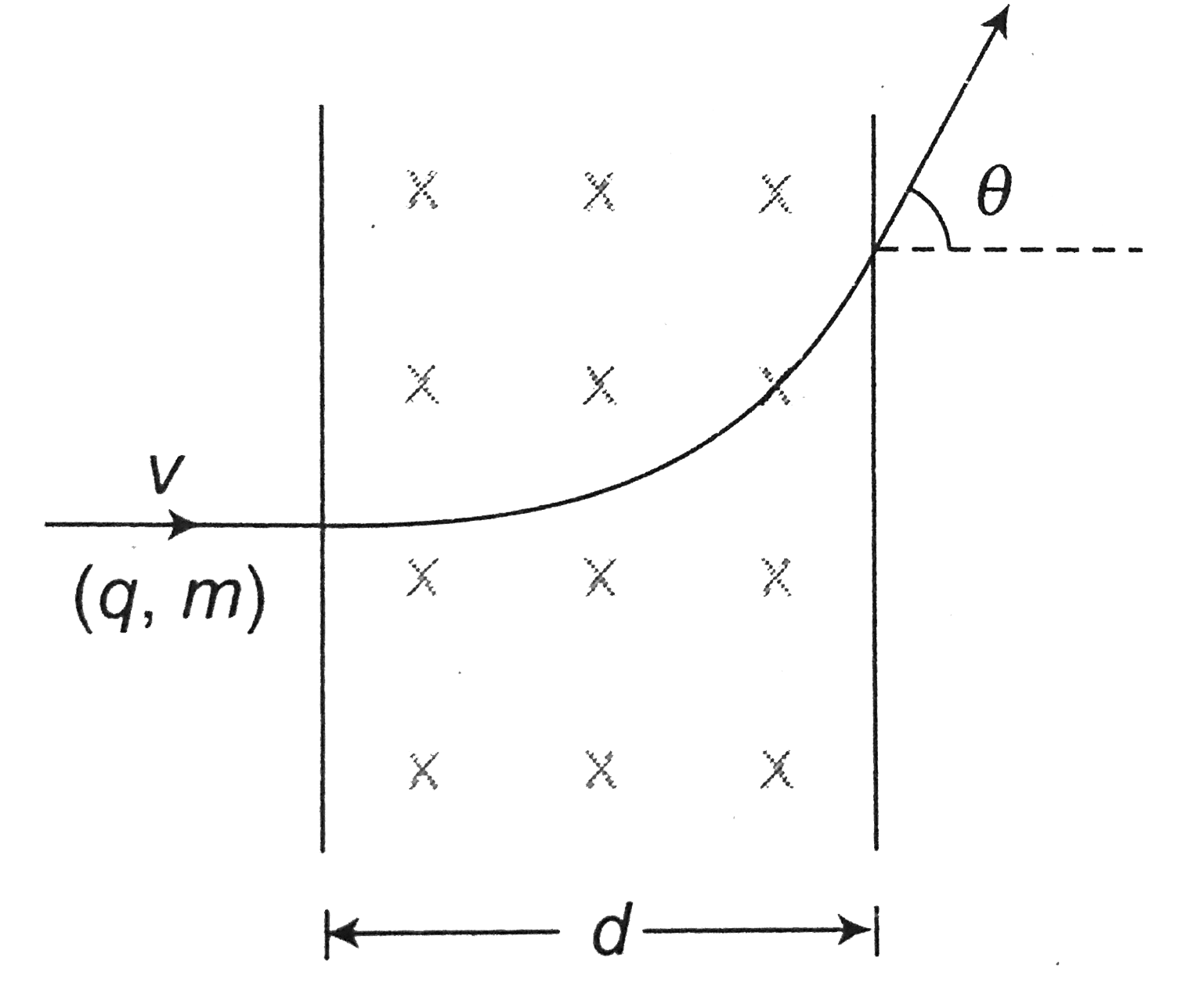
View SolutionPositively charged particles are projected into a magnetic field. If the direction of the magnetic field is along the direction of motion of the charged particles, the particles get
View Solution
Knowledge Check
A charged particle of mass m and charge q enters a magnetic field B with a velocity v at an angle θ with the direction of B. The radius fo the resulting path is
AmvsinθqBBmvqBsinθCmvqBDmvtanθqBA charged particle of charge q and mass m is shot into a uniform magnetic field of induction B at an angle θ with the field. The frequency of revolution of the particle
ADepends on the angle θBIs independent of the angle θCIs proportional to the specific charge q/m of the particleDIs inversely proportional to the value of BAn electric charge q is moving with a velocity w in the direction of a magnetic field B. The magnetic force acting on the charge is
AqvBBzeroCqvBDvqB
Write the expression for the magnetic force acting on a, charged particle moving with velocity v in the presence of magnetic field B.
View SolutionA charged particle enters a region of uniform magnetic field at an angle of 85∘ to the magnetic line of force . The path of the particle is a circle .
View SolutionDiscuss the motion of a charged particle when subjected to a uniform magnetic field, when the direction of motion of the particle makes an angle ϕ with the direction of magnetic field.
View SolutionA charged particle enters into a magnetic field with velocity vector making an angle of 30∘ with respect of the direction of magnetic field. The path of the particle is
View SolutionPositively charged particles are projected into a magnetic field. If the direction of the magnetic field is along the direction of motion of the charged particles, the particles get
View Solution
