The energy of a photon is equal to the kinetic energy of a proton.The energy of the photon is E.Let λ1 be de-Broglie wavelength of the proton and λ2 be the waveelength of the photon.The ratio λ1/λ2 is proportional toSolution in Punjabi
E0
E1/2
E−1
E−2.
Step by step video & image solution for The energy of a photon is equal to the kinetic energy of a proton.The energy of the photon is E.Let lambda_1 be de-Broglie wavelength of the proton and lambda_2 be the waveelength of the photon.The ratio lambda_1//lambda_2 is proportional to by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
Similar Questions
The photon of frequency v has a momntum associated with it .If c is the velocity of light,then momentum is
02:16View SolutionTo get five images of a single object, one should have two plane mirrors at an angle of :
02:56View SolutionProve that electromagnetic waves are transverse in nature.
01:54View SolutionThe energy of a photon is equal to the kinetic energy of a proton. The energy of the photon is E. Let lambda_1 be the de-Broglie wavelength of the proton and lambda_2 be the wavelength of the photon. The ratio (lambda_1)/(lambda_2) is proportional to (a) E^0 (b) E^(1//2) (c ) E^(-1) (d) E^(-2)
02:57View SolutionThe potential energy of a partical varies as
. U(x)=E0for0≤x≤1 =0forx>1For0≤x≤1, de- Broglie wavelength is λ1 and for xgt the de-Broglie wavelength is λ2. Total energy of the partical is 2E_0. find λ1λ2.03:28View SolutionTwo protons are having same kinetic energy. One proton enters a uniform magnetic field at right angles ot it. Second proton enters a uniform electric field in the direction of field. After some time their de Broglie wavelengths are lambda_1 and lambda_2 then (a) lambda_1 = lambda_2 (b) lambda_1 lt lambda_2 (c) lambda_1 gt lambda_2 (d) some more information is required
01:43View SolutionThe energy of a photon is equal to the kinetic energy of a proton. If λ1 is the de-Broglie wavelength of a proton, λ2 the wavelength associated with the proton and if the energy of the photon is E, then (λ1/λ2) is proportional to
03:17View Solutionthe energy of photon is equal to the kinetic energy of a porton,If lambda_1 is the De-Broglie wavelength of a proton, lambda_2 the wavelength associated with the proton and if the energt of the protonis E, then (lamda_1//lambda_2) is proportional to
01:50View SolutionWhen kinetic energy of proton is equal to energy of photon then ratio of de-Broglie wavelength of proton and photon is proportional to …..
View SolutionThe maximum kinetic energy of photoelectron is doubled when the wavelength of light incident on the photosensitive changes from λ1 to λ2. Deduce expression for the threshold wavelength and work function for metals in terms of λ1 and λ2
04:38View SolutionWhen an electron is transisted from 2E to E energy level, the wavelength of resultant photon produce is λ. If electronic transition involves 43 E to e level, the wavelength of resultant photon is λ2. The correct relation between λ1 & λ2 is λ2=xλ1. Then find the value of x ?
03:14View SolutionThe energy of a photon is equal to the kinetic energy of a proton. If λ1 is the de Broglie wavelength of a proton, λ2 the wavelength associated with the photon, and if the energy of the photon is E, then (λ1/λ2) is proportional to
01:08View Solutionλ1 तरंगदैर्ध्य के प्रकाश से उत्सर्जित फोटो इलेक्ट्रान की अधिकतम गतिज उर्जा K1 एवं λ2 के लिये K2 है। यदि λ1=2λ2 हो तब
02:28View Solutionएक परमाणु के तीन ऊर्जा स्तर चित्र में दिखाये गये है। तीन सम्भव विकरण से सम्बन्धित तरंगदैर्ध्य λ1,λ2 और λ3 का मान λ1 और λ2 के पदों में दिया जा सकता है।__________
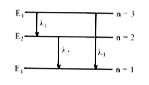 01:56View Solution
01:56View SolutionThe energy of a photon is equal to the kinetic energy of a proton. The energy of the photon is E. Let lambda_1 be the de-Broglie wavelength of the proton and lambda_2 be the wavelength of the photon. The ratio (lambda_1)/(lambda_2) is proportional to (a) E^0 (b) E^(1//2) (c ) E^(-1) (d) E^(-2)
04:51View SolutionThe potential energy of a partical varies as
. U(x)=E0for0≤x≤1 =0forx>1For0≤x≤1, de- Broglie wavelength is λ1 and for xgt the de-Broglie wavelength is λ2. Total energy of the partical is 2E_0. find λ1λ2.03:58View Solution

