A chord of a circle of radius 6 cm subtends an angle of 60∘ at the centre of the circle. The area of the minor segment is (useπ=3.14)
6.54cm2
0.327cm2
7.25cm2
3.27cm2
To find the area of the minor segment of a circle with a radius of 6 cm that subtends an angle of 60 degrees at the center, we can follow these steps:
Step 1: Understand the formula for the area of the minor segment
The area of the minor segment can be calculated using the formula:
Area of minor segment=θ360πr2−12r2sin(θ)
where:
- θ is the angle in degrees,
- r is the radius of the circle.
Step 2: Substitute the known values into the formula
Given:
- θ=60∘
- r=6 cm
- π≈3.14
Substituting these values into the formula:
Area of minor segment=60360×3.14×(6)2−12×(6)2×sin(60∘)
Step 3: Calculate each part of the formula
1. Calculate 60360:
60360=16
2. Calculate r2:
(6)2=36
3. Calculate the first term:
16×3.14×36=113.046=18.84 cm2
4. Calculate sin(60∘):
sin(60∘)=√32≈0.866
5. Calculate the second term:
12×36×0.866=18×0.866=15.588 cm2
Step 4: Combine the results to find the area of the minor segment
Now, substitute back into the formula:
Area of minor segment=18.84−15.588=3.252 cm2
Step 5: Round the answer
Rounding to two decimal places, we get:
Area of minor segment≈3.25 cm2
Final Answer
The area of the minor segment is approximately 3.25 cm2.
The area of the minor segment can be calculated using the formula:
Area of minor segment=θ360πr2−12r2sin(θ)
where:
- θ is the angle in degrees,
- r is the radius of the circle.
Given:
- θ=60∘
- r=6 cm
- π≈3.14
Area of minor segment=60360×3.14×(6)2−12×(6)2×sin(60∘)
1. Calculate 60360:
60360=16
(6)2=36
16×3.14×36=113.046=18.84 cm2
sin(60∘)=√32≈0.866
12×36×0.866=18×0.866=15.588 cm2
Now, substitute back into the formula:
Area of minor segment=18.84−15.588=3.252 cm2
Rounding to two decimal places, we get:
Area of minor segment≈3.25 cm2
The area of the minor segment is approximately 3.25 cm2.
Similar Questions
A chord of a circle of radius 30 cm makes an angle of 60∘ at the centre of the circle. Find the areas of the major segment. [Take π=3.14 and √3=1.732]
View SolutionA chord AB of a circle, of radius 14 cm makes an angle of 60∘ at the centre of the circle. Find the area of the minor segment of the circle.
View Solution
Knowledge Check
A chord of a circle of radius 10cm subtends a right angle at the centre. The area of the minor segments (given π=3.14) is
A32.5cm2B34.5cm2C28.5cm2D30.5cm2
A chord PQ of a circle with radius 15 cm subtends an angle of 60∘ with the centre of the circle. Find the area of the minor as well as the major segment. (π=3.14,√3=1.73)
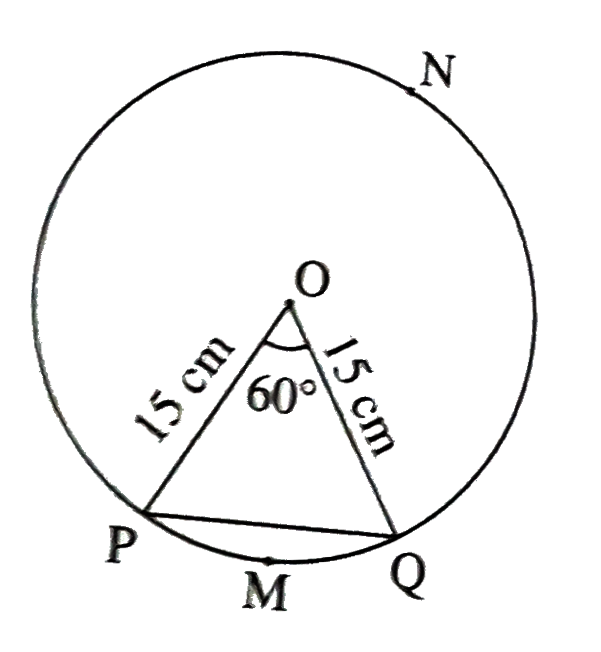
View SolutionA chord PQ of a circle4 with radius 15 cm subtends an angle of 60∘ with the centre of the circle.
Find the area of the inor as well as the major segement. (π=3.14,√3=1.73)
Given: r=15cm, θ=60∘
To find A(minor segment)
A(major segment)
View SolutionA chord AB of a circle of radius 15 cm makes an angle of 60o at the centre of the circle. Find the area of the major and minor segment. (Take π=3.14, √3=1.73)
View SolutionA chord of a circle of radius 30 cm makes an angle of 60∘ at the centre of the circle. Find the areas of the minor and major segments. [Take π=314 and √3=1.732]
View SolutionA chord PQ of a circle of radius 10 cm makes an angle of 60∘ at the centre of the circle. Find the area of the major and the minor segment
View SolutionA chord of a circle of radius 14 cm subtends a right angle at the centre. The area of the minor segments (given π = 3.14 ) is
View SolutionA chord AB of a circle of radius 10cm makes a right angle at the centre of the circle. Find the area of the major and minor segments (Take π=3.14).
View Solution
