The shadow of a standing tower of height 2575 m is found to be 50 m longer when the sun’s elevation changes from to . Find the measure of X
(a)
(b)
(c)
(d)
To solve the problem, we need to find the angle x when the shadow of a tower changes as the sun's elevation changes. Let's break it down step by step.
Step 1: Understand the problem
We have a tower of height h=2575 m. When the sun's elevation is 60∘, the shadow length is L. When the elevation changes to x∘, the shadow length becomes L+50 m.
Step 2: Set up the equations using trigonometry
Using the tangent function for the angle of elevation, we can set up two equations based on the two angles.
1. For the angle 60∘:
tan(60∘)=hL
We know that tan(60∘)=√3, so:
√3=2575L
Rearranging gives us:
L=2575√3
2. For the angle x∘:
tan(x)=hL+50
Thus:
tan(x)=2575L+50
Step 3: Substitute L into the second equation
Substituting L from the first equation into the second:
tan(x)=25752575√3+50
Simplifying the denominator:
tan(x)=25752575+50√3√3
This simplifies to:
tan(x)=2575⋅√32575+50√3
Step 4: Solve for x
Now we need to find x such that:
tan(x)=2575⋅√32575+50√3
Step 5: Calculate the value of x
To find x, we can use a calculator or trigonometric tables to find the angle whose tangent is equal to the value we computed.
Calculating the right-hand side:
1. Calculate 2575+50√3 (approximately 2575+86.6≈2661.6).
2. Calculate 2575⋅√32661.6 (approximately 2575⋅1.7322661.6≈1.75).
3. Find x such that tan(x)≈1.75.
Using a calculator:
x≈60∘+15∘=75∘
Conclusion
Thus, the measure of x is 75∘.
We have a tower of height h=2575 m. When the sun's elevation is 60∘, the shadow length is L. When the elevation changes to x∘, the shadow length becomes L+50 m.
Using the tangent function for the angle of elevation, we can set up two equations based on the two angles.
tan(60∘)=hL
We know that tan(60∘)=√3, so:
√3=2575L
Rearranging gives us:
L=2575√3
tan(x)=hL+50
Thus:
tan(x)=2575L+50
Substituting L from the first equation into the second:
tan(x)=25752575√3+50
Simplifying the denominator:
tan(x)=25752575+50√3√3
This simplifies to:
tan(x)=2575⋅√32575+50√3
Now we need to find x such that:
tan(x)=2575⋅√32575+50√3
To find x, we can use a calculator or trigonometric tables to find the angle whose tangent is equal to the value we computed.
1. Calculate 2575+50√3 (approximately 2575+86.6≈2661.6).
2. Calculate 2575⋅√32661.6 (approximately 2575⋅1.7322661.6≈1.75).
3. Find x such that tan(x)≈1.75.
x≈60∘+15∘=75∘
Thus, the measure of x is 75∘.
Similar Questions
The shadow of a tower standing on a level plane is found to be 50 m longer when when sun's elevation is 30∘ than when it is 60∘. Find the height of the tower.
View SolutionThe shadow of a tower is found to be x metre longer, when the angle of elevation of the sun changes from 60∘ to 45∘. If the height of the tower is 5(3+√3)m, then what is x equal to ?
View Solution
Knowledge Check
The shadow of a tower standing on a level plane is found to be 40 m longer when the sun 's altitude is 45∘ , than when it is 60∘ . The height of the tower is
A644 mB66.644 mC54.644 mD76.644 mThe shadow of a tower standing on a level plane is found to be 50 m longer when the Sun's elevation is 30∘ than when it is 60∘. The height of the tower is
AA. 25 mBB. 25√3mCC. 50mDD. None of theseThe shadow of a tower standing on a level plane is found to be 50m longer when sun's altitude is 30∘ then when it is 60∘. Find the height of tower.
A25 mB25√3mC25√3D30m
The shadow of a tower standing on a level plane is found to be 50 m longer when the Sun's elevation is 30∘ than when it is 60∘ What is the height of the tower ?
View SolutionThe shadow of a tower standing on a level ground is found to be 20 m longer when the sun's altitude is 45∘ than when it is 60∘ .Find the height of the tower .
View SolutionThe shadow of a tower standing in a level plane is found to be 18 m shorter when the sun's altitude changes from 30∘ to 45∘. Show that the height of the tower is 9(1+√3)m.
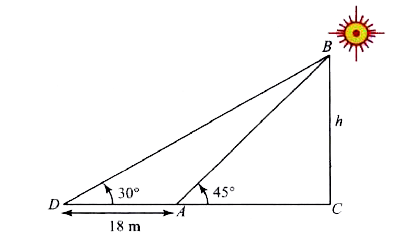
View SolutionThe shadow of a tower standing on a level plane is found to be 50 m longer when the Sun's elevation is 30∘ than when it is 60∘ What is the height of the tower ?
View SolutionThe shadow of a tower is found to be 60 m shorter when the Sun’s altitude change from 30∘ to 60∘.The height of the power from the ground is approximately
View Solution
