Derive an expression for field intensity due to an electric dipole in vacuum for points on its axis . Compare the variation of field intensity with distance for an electric dipole and a point charge when both are kept in vacuum .
Text Solution
At a Point on the Axial Line we have to calculate the field intensity E at a point P on the axial line of the dipole and at a distance OP = x , from the centre O of the dipole .
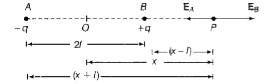
Electric field on axial line of an electric dipole
Resultant electric field intensity at the point P is Ep=EA+EB
The vectors EA and EB are collinear and opposite .
∴EP=EB−EA
Here , EA=14πε0⋅q(x+l)2
∴Ep=14πε0[q(x−l)2−q(x+l)2]
=14πε0⋅4qlx(x2−l2)2
Since , we know p = q⋅2l
Hence , Ep=14πε0⋅2px(x2−l2)2
If dipole is short 2l<<x , then
Ep=2p4πε0x3 ....(i)
The direction of Ep is along BP produced .
Clearly Ep∝1x3
The electric field due to a dipole falls off at large distance at a much greater rate
(E∝1r3) than the electric field due to a single charge (E∝1r2) .
|
Similar Questions
Knowledge Check
Electric field intensity (E) due to an electric dipole varies with distance (r) from the point of the center of dipole as :
AE∝1rBE∝1r4CE∝1r2DE∝1r3Electric field intensity (E) due to an electric dipole varies with distance (r) of the point from the center of dipole as :
AE∝1rBE∝1r4CE∝1r2DE∝1r3Electric field intensity (E) due to an electric dipole varies with distance (r ) from the point of the center of dipole as :
AE∝1rBE∝1r4CE∝1r2DE∝1r3
The direction of the electric field intensity due to an electric dipole at a point on its axis is the same as the direction of _____
View SolutionDerive an expression for intensity of electric field are a point in broadside position or on an equatorial line of an electric dipole.
View SolutionDeduce an expression for the electric potential due to an electric dipole at any point on its axis. Mention one contrasting feature of electric potential at a point due to dipole as compared to that due to a single charge.
View SolutionDerive an expression for the electric field intensity at a point outside a charged conducting sphere.
View SolutionElectric field intensity (E) due to an electric dipole varies with distance (r ) from the point of the center of dipole as :
View Solution
