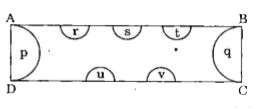
Seven semi-circular areas are removed from the rectangle ABCD as shown in the figure above, in which AB = 2 cm and AD = 0.5 cm. The radius of each semi-circle r, s, t, u, v is half of that of semi-circle p or q. What is the area of the remaining portion ?
(128−13π)/128cm2
(125−13π)/125cm2
(128−15π)/128cm2
None of the above
Step by step video & image solution for Seven semi-circular areas are removed from the rectangle ABCD as shown in the figure above, in which AB = 2 cm and AD = 0.5 cm. The radius of each semi-circle r, s, t, u, v is half of that of semi-circle p or q. What is the area of the remaining portion ? by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Similar Questions
Knowledge Check
- Question 1 - Select One
In the following figure AB=BC and AC=84 cm. The radius of the inscribed circle is 14 cm. B is the centre of the largest semi-circle . What is the area of the shaded region ?
 A335cm2B770cm2C840cm2D650cm2
A335cm2B770cm2C840cm2D650cm2 - Question 2 - Select One
In the figure , triangle ABC is isosceles in which AB = AC = 6 cm . If the radius of circle is 9 cm then what is the area of the triangle?
A8√2cm2B8cm2C2√2cm2D8√2cm2 - Question 3 - Select One
The radius of a circle is increased by 2cm from 5 cm to 7 cm . What is the percentage change in area of the circle ?
A96%B35%C70%D74%
ABCP is a quadrant of a circle of radius 14 cm. With AC as diameter, a semi-circle is drawn. Find the area of the shaded portion.
View SolutionA sheet of paper is in the form of a rectangle ABCD in which AB=40cm and AD=28cm . A semi-circular portion with BC as diameter is cut off. Find the area of the remaining paper.
View SolutionThree circle of equal radii touch each other as shown in figure . The radius of each circle is 1 cm. What is the area of shaded region ?
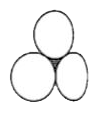 View Solution
View SolutionThe radius of a circle is increased by 2cm from 5 cm to 7 cm . What is the percentage change in area of the circle ?
View SolutionThe figure shows a rectangle ABCD with a semi-circle and a circle inscribed inside it as shown. What is the ratio of the area of the circle to that of the semi-circle ?
 View Solution
View Solution

