The remainder on dividing given integers a and h by 7 are respectively 5 and 4. What is the remainder when ab is divided by 7 ?
3
4
5
6
To solve the problem, we need to find the remainder when the product ab is divided by 7, given that the remainders of a and b when divided by 7 are 5 and 4, respectively.
1. Understand the Remainders:
- We know that a≡5mod7 (which means when a is divided by 7, the remainder is 5).
- We also know that b≡4mod7 (which means when b is divided by 7, the remainder is 4).
2. Express a and b:
- From the above, we can express a and b in terms of some integers k and m:
- a=7k+5 for some integer k
- b=7m+4 for some integer m
3. Calculate the Product ab:
- Now, we calculate the product ab:
ab=(7k+5)(7m+4)
- Expanding this:
ab=49km+28k+35m+20
4. Find the Remainder when Dividing by 7:
- Now, we need to find abmod7. We can simplify each term in the product modulo 7:
- 49kmmod7≡0 (since 49 is a multiple of 7)
- 28kmod7≡0 (since 28 is a multiple of 7)
- 35mmod7≡0 (since 35 is a multiple of 7)
- 20mod7≡6 (since 20=2×7+6)
5. Combine the Results:
- Therefore, when we combine these results, we have:
abmod7≡0+0+0+6≡6mod7
6. Conclusion:
- The remainder when ab is divided by 7 is 6.
- We know that a≡5mod7 (which means when a is divided by 7, the remainder is 5).
- We also know that b≡4mod7 (which means when b is divided by 7, the remainder is 4).
- From the above, we can express a and b in terms of some integers k and m:
- a=7k+5 for some integer k
- b=7m+4 for some integer m
- Now, we calculate the product ab:
ab=(7k+5)(7m+4)
- Expanding this:
ab=49km+28k+35m+20
- Now, we need to find abmod7. We can simplify each term in the product modulo 7:
- 49kmmod7≡0 (since 49 is a multiple of 7)
- 28kmod7≡0 (since 28 is a multiple of 7)
- 35mmod7≡0 (since 35 is a multiple of 7)
- 20mod7≡6 (since 20=2×7+6)
- Therefore, when we combine these results, we have:
abmod7≡0+0+0+6≡6mod7
- The remainder when ab is divided by 7 is 6.
Similar Questions
Knowledge Check
What is the remainder when 41000 is divided by 7 ?
A1B4C2D6
What is the remainder when 22012 is divided by 7 ?
View SolutionWhat is the remainder when 781 is divided by 5
View SolutionWhat is the remainder when 41000 is divided by 7?
View SolutionRemainder when
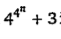 is divided by 7 is:
is divided by 7 is:
View SolutionWhat is the remainder when 21000000 is divided by 7?
View SolutionFind the remainder when 118 is divided by 7.
View SolutionFind the remainder when 77 is divided by 4.
View Solution
