The following sets of conditions relate to two triangles ABC and DEF. Which set of conditions does' not guarantee the congruence of ABC and DEF ?
a=d, b=e, c=f
∠B=∠E,∠C=∠F,a=d
c=f,b=e,∠A=∠D
c=f,b=e,∠B=∠E
To determine which set of conditions does not guarantee the congruence of triangles ABC and DEF, we need to analyze the given conditions based on the criteria for triangle congruence. The main criteria for triangle congruence are:
1. Side-Side-Side (SSS): If all three sides of one triangle are equal to the three sides of another triangle, then the triangles are congruent.
2. Angle-Side-Angle (ASA): If two angles and the included side of one triangle are equal to two angles and the included side of another triangle, then the triangles are congruent.
3. Side-Angle-Side (SAS): If two sides and the included angle of one triangle are equal to two sides and the included angle of another triangle, then the triangles are congruent.
4. Angle-Angle-Side (AAS): If two angles and a non-included side of one triangle are equal to two angles and a non-included side of another triangle, then the triangles are congruent.
Now, let’s analyze the conditions provided in the question step by step:
Step 1: Analyze the First Condition (SSS)
- If all three sides of triangle ABC are equal to the corresponding sides of triangle DEF (i.e., AB = DE, BC = EF, AC = DF), then the triangles are congruent by the SSS criterion.
- Conclusion: This condition guarantees congruence.
Step 2: Analyze the Second Condition (ASA)
- If angle B = angle E and angle C = angle F, and side AC = side DF, then triangles ABC and DEF are congruent by the ASA criterion.
- Conclusion: This condition guarantees congruence.
Step 3: Analyze the Third Condition (SAS)
- If side AB = side DE, angle B = angle E, and side BC = side EF, then triangles ABC and DEF are congruent by the SAS criterion.
- Conclusion: This condition guarantees congruence.
Step 4: Analyze the Fourth Condition (AAS)
- If side AC = side DF, side BC = side EF, and angle B = angle E, then this does not guarantee congruence because it does not specify the relationship of the included angle between the two sides.
- Conclusion: This condition does not guarantee congruence.
Final Answer
The set of conditions that does not guarantee the congruence of triangles ABC and DEF is the fourth condition.
---
2. Angle-Side-Angle (ASA): If two angles and the included side of one triangle are equal to two angles and the included side of another triangle, then the triangles are congruent.
3. Side-Angle-Side (SAS): If two sides and the included angle of one triangle are equal to two sides and the included angle of another triangle, then the triangles are congruent.
4. Angle-Angle-Side (AAS): If two angles and a non-included side of one triangle are equal to two angles and a non-included side of another triangle, then the triangles are congruent.
- If all three sides of triangle ABC are equal to the corresponding sides of triangle DEF (i.e., AB = DE, BC = EF, AC = DF), then the triangles are congruent by the SSS criterion.
- Conclusion: This condition guarantees congruence.
- If angle B = angle E and angle C = angle F, and side AC = side DF, then triangles ABC and DEF are congruent by the ASA criterion.
- Conclusion: This condition guarantees congruence.
- If side AB = side DE, angle B = angle E, and side BC = side EF, then triangles ABC and DEF are congruent by the SAS criterion.
- Conclusion: This condition guarantees congruence.
- If side AC = side DF, side BC = side EF, and angle B = angle E, then this does not guarantee congruence because it does not specify the relationship of the included angle between the two sides.
- Conclusion: This condition does not guarantee congruence.
The set of conditions that does not guarantee the congruence of triangles ABC and DEF is the fourth condition.
Similar Questions
Knowledge Check
Consider the two similar triangles ABC and DEF. Which of the following is correct about the ratio of the area of the triangle ABCandDEF ?
A(ABDE)=(EFBC)=(ACDF)B(ABDE)2=(BCEF)2=(ACDF)2C(ABDE)=(BCEF)=(DFAC)DNone of theseConsider the two similar triangles ABC and DEF. Which of the following is correct about the ratio of the area of the triangle ABCandDEF ?
A(ABDE)=(EFBC)=(ACDF)B(ABDE)2=(BCEF)2=(ACDF)2C(ABDE)=(BCEF)=(DFAC)DNone of theseIf △ABC≅△DEF then
AAC=DEBBC=DFCFE=CBDAB=DF
The corresponding altitudes of two similar triangles are 6 cm and 9 cm respectively Find the ratio of the area of △ABC and △DEF
View SolutionWhich of the following is the correct option for the congruency of the two triangles ABC and PQR as per the SAS congruency criterion ?
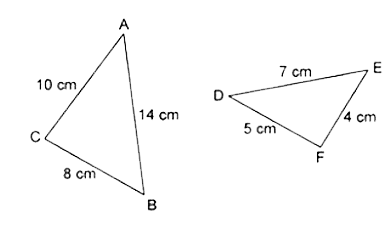
View SolutionWhich of [he following condition is TRUE about the similarity of triangle ABC and DEF given below?
View SolutionIn two triangle ABC and DEF, AB= DE ,BC=DF and AC =Ef then
View SolutionIn two triangles ABC an DEF,∠A=∠D. The sum of the angles A and B is equal to the sum of the angles D and E. If BC=6 cm and EF=8cm, find the ratio of the areas of the triangles, ABC and DEF.
View Solution