Question

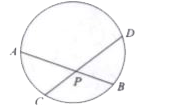
Two circles touch each other externally at P. Two secants APB and CPD are drawn through P to meet the circle at A, C and B, D respectively. Then, which one of the following is correct ?

Options

A. AC is perpendicular to BD
B. AC intersects BD
C. AC is parallel to BD
D. None of the above

Explanation

To solve the problem, we need to analyze the given situation involving two circles that touch each other externally at point P, and two secants APB and CPD drawn through P.

1. Understanding the Configuration:
- We have two circles that touch each other externally at point P.
- Two secants APB and CPD are drawn through point P, intersecting the circles at points A, B and C, D respectively.

Hint: Visualize the two circles and the secants to understand their relationships.

2. Identifying Angles:
- Let’s denote the angles formed by the secants at point P.
- The angle ∠APB is formed by secant APB and the angle ∠CPD is formed by secant CPD.

Hint: Remember that angles formed by two intersecting lines can provide important relationships.

3. Using the Property of Tangents:
- Since the circles touch each other externally at point P, the angles formed by the secants at point P will have specific relationships.
- Specifically, the angle ∠APN (where N is the point of tangency on the larger circle) will be equal to the angle ∠CPM (where M is the point of tangency on the smaller circle).

Hint: Recall the property that angles formed by a tangent and a chord through the point of contact are equal to the angles in the alternate segment.

4. Establishing Angle Relationships:
- From the above, we conclude that ∠APN = ∠CPM.
- Similarly, we can establish that ∠BPM (for the larger circle) is equal to ∠DPN (for the smaller circle).
- Thus, we have:
- ∠APN = ∠CPM
- ∠BPM = ∠DPN

Hint: Use the properties of angles in triangles and circles to establish equalities.

5. Applying the Triangle Angle Sum Property:
- In triangles ACP and BDP, we can see that:
- ∠APN = ∠BPM and ∠CPM = ∠DPN.
- Therefore, if two angles of triangle ACP are equal to two angles of triangle BDP, the triangles are similar.

Hint: Remember that if two angles of one triangle are equal to two angles of another triangle, the triangles are similar.

6. Concluding Parallel Lines:
- Since the corresponding angles of the triangles ACP and BDP are equal, we can conclude that the lines AC and BD are parallel (by the converse of the alternate angle theorem).
- Therefore, we have AC || BD.

Hint: Use the concept of alternate angles to conclude the parallelism of the lines.

Final Answer:
The correct option is that AC is parallel to BD.