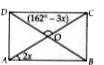
If a side AB of a rectangle ABCD is divided equally at in 4 parts by points x, y and z, find
area of Δxycarea of rectangle ABCD=?

17
16
19
18
The correct Answer is:D
Step by step video, text & image solution for If a side AB of a rectangle ABCD is divided equally at in 4 parts by points x, y and z, find ("area of "Delta"xyc")/("area of rectangle ABCD")=? by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Updated on:21/07/2023Topper's Solved these Questions
- QUADRILATERAL BOOK - LUCENT PUBLICATIONCHAPTER - QUADRILATERAL EXERCISE - Exercise 7A
31 Videos
- LINES AND ANGLES BOOK - LUCENT PUBLICATIONCHAPTER - LINES AND ANGLES EXERCISE - EXERCISE 4B
5 Videos
- TRIGONOMETRIC RATIO OF SPECIFIC ANGLESBOOK - LUCENT PUBLICATIONCHAPTER - TRIGONOMETRIC RATIO OF SPECIFIC ANGLESEXERCISE - Exercise 10B
10 Videos
Similar Questions
Knowledge Check
Side AB of rectangle of ABCD is divided into four equal parts by points x, y , z . The ratio of the area(ΔXYC)Area (Rectangle ABCD) is
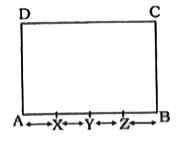 A17B16C19D18
A17B16C19D18If P is a point within a rectangle ABCD, then:
AAP2+PC2=BP2+PD2BAP2+BP2=PC2+PD2CAP+PC=BP+PDDAP×PC=BP×PDIf P is a point within a rectangle ABCD, then:
AAP2+PC2=BP2+PD2BAP2+BP2=PC2+PD2CAP+PC=BP+PDDAP×PC=BP×PD
Segments starting with points M and N and ending with vertices of the rectangle ABCD divide the given figure into eight parts (see in the figure). The areas of three parts of the rectangle are indicated in the picture. What is the area of the shaded region
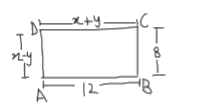
View SolutionIf ABCD is a rectangle , find the values of x and y
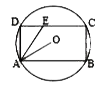
View SolutionIn given figure, a rectangle ABCD is inside a circle. Side AB is greater than BC. The ratio of area of circle to rectangle aBCD is π:√3 Line segment AE intersect CD at E where ∠OAB=∠EAD . Find the ratio of AE to AD .
View Solution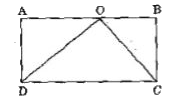
In the figure given above, the area of rectangle ABCD is 100 square cm, O is any point on AB and CD = 20 cm. Then the area of triangle COD ia
View SolutionOne of the diameters of the circle circumscribing the rectangle ABCD is 4y=x+y. If AandB are the points (−3,4)and(5,4) respectively, find the area of the rectangle and equation of the circle.
View Solution