If a.(b×c)=0, then the correct statement is
out of a, b, c, any two vectors are parallel
a, b, c are coplanar
any two are equal among a,b,c
atleast one statement is correct
The correct Answer is:B
To solve the problem, we need to analyze the given condition a⋅(b×c)=0 and determine the implications of this condition regarding the vectors involved.
1. Understanding the Scalar Triple Product:
The expression a⋅(b×c) represents the scalar triple product of the vectors a,b, and c.
2. Condition for Coplanarity:
The scalar triple product a⋅(b×c)=0 indicates that the volume of the parallelepiped formed by the vectors a,b, and c is zero. This occurs if and only if the vectors are coplanar.
3. Conclusion:
Since the scalar triple product is zero, we conclude that the vectors a,b, and c are coplanar.
4. Evaluating Options:
- Option 1: Any two vectors are parallel. (Not necessarily true)
- Option 2: a,b,c are coplanar. (True)
- Option 3: Any two are equal among a,b,c. (Not necessarily true)
- Option 4: None of the above. (False since option 2 is true)
Thus, the correct statement is that a,b,c are coplanar.
Final Answer:
The correct statement is: a,b,c are coplanar.
---
The expression a⋅(b×c) represents the scalar triple product of the vectors a,b, and c.
The scalar triple product a⋅(b×c)=0 indicates that the volume of the parallelepiped formed by the vectors a,b, and c is zero. This occurs if and only if the vectors are coplanar.
Since the scalar triple product is zero, we conclude that the vectors a,b, and c are coplanar.
- Option 1: Any two vectors are parallel. (Not necessarily true)
- Option 2: a,b,c are coplanar. (True)
- Option 3: Any two are equal among a,b,c. (Not necessarily true)
- Option 4: None of the above. (False since option 2 is true)
The correct statement is: a,b,c are coplanar.
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
If →aand→b are two vectors such that →a.→b=0and→a×→b=0, then which one of the following is correct?
Aa is parallel to bBa is perpendicular to bCeither a=0orb=0Dnone of these - Question 2 - Select One
If A = [ a,b] , B = [ - b, -a] and C=[a.−a] then the correct statement is
AA = -ABA + B = A-BCAC = BCDCA = CB - Question 3 - Select One
If a×b=c×b≠0, then
Aa=λbBa−b=λcC(a−c)=λbDnone
Cordinates of the vertices of the triangle ABC are A(12,8),B(−2,6),C(6,0) then the correct statement is:
View SolutionCordinates of the vertices of the triangle ABC are A(12,8),B(−2,6),C(6,0) then the correct statement is:
View SolutionCordinates of the vertices of the triangle ABC are A(12,8),B(−2,6),C(6,0) then the correct statement is:
View SolutionIdentify A , B and C in the image and choose the correct statement.
 View Solution
View SolutionIn the circuit shown below, the key is pressed at time t = 0. The correct statement is
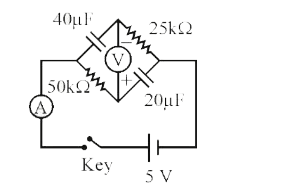 View Solution
View Solution

