OPQR is a square with M and N as the middle points of the sides PQ and QR, respectively. The ratio of the areas of the square and the triangle OMN is
4:1
2:1
8:3
4:3
The correct Answer is:C
Step by step video, text & image solution for OPQR is a square with M and N as the middle points of the sides PQ and QR, respectively. The ratio of the areas of the square and the triangle OMN is by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
Similar Questions
OPQR is a square and M,N are the middle points of the sides PQandQR , respectively. Then the ratio of the area of the square to that of triangle OMN is 4:1 (b) 2:1 (c) 8:3 (d) 7:3
View SolutionOPQR is a square and M,N are the midpoints of the sides PQ and QR , respectively. If the ratio of the area of the square to that of triangle OMN is λ:6, then λ4 is equal to 2 (b) 4 (c) 2 (d) 16
View Solution
Knowledge Check
- Question 1 - Select One
OPQR is a square with M and N as the middle points of the sides PQ and QR, respectively. The ratio of the areas of the square and the triangle OMN is
A4:1B2:1C8:3D4:3 - Question 2 - Select One
Let □PQRS be a quadrilateral. If M and N are the mid-points of the sides PQ and RS respectively, then PS+QR=
A3¯¯¯¯¯¯¯¯MNB4¯¯¯¯¯¯¯¯MNC2¯¯¯¯¯¯¯¯MND2¯¯¯¯¯¯¯¯NM - Question 3 - Select One
PQRS is a square with side 10 cm. A, B, C and D are mid-points of PQ, QR, RS and SP respectively. Then the perimeter of the square ABCD so formed is
A10√2cmB20√2cmC25√2cmD15√2cm
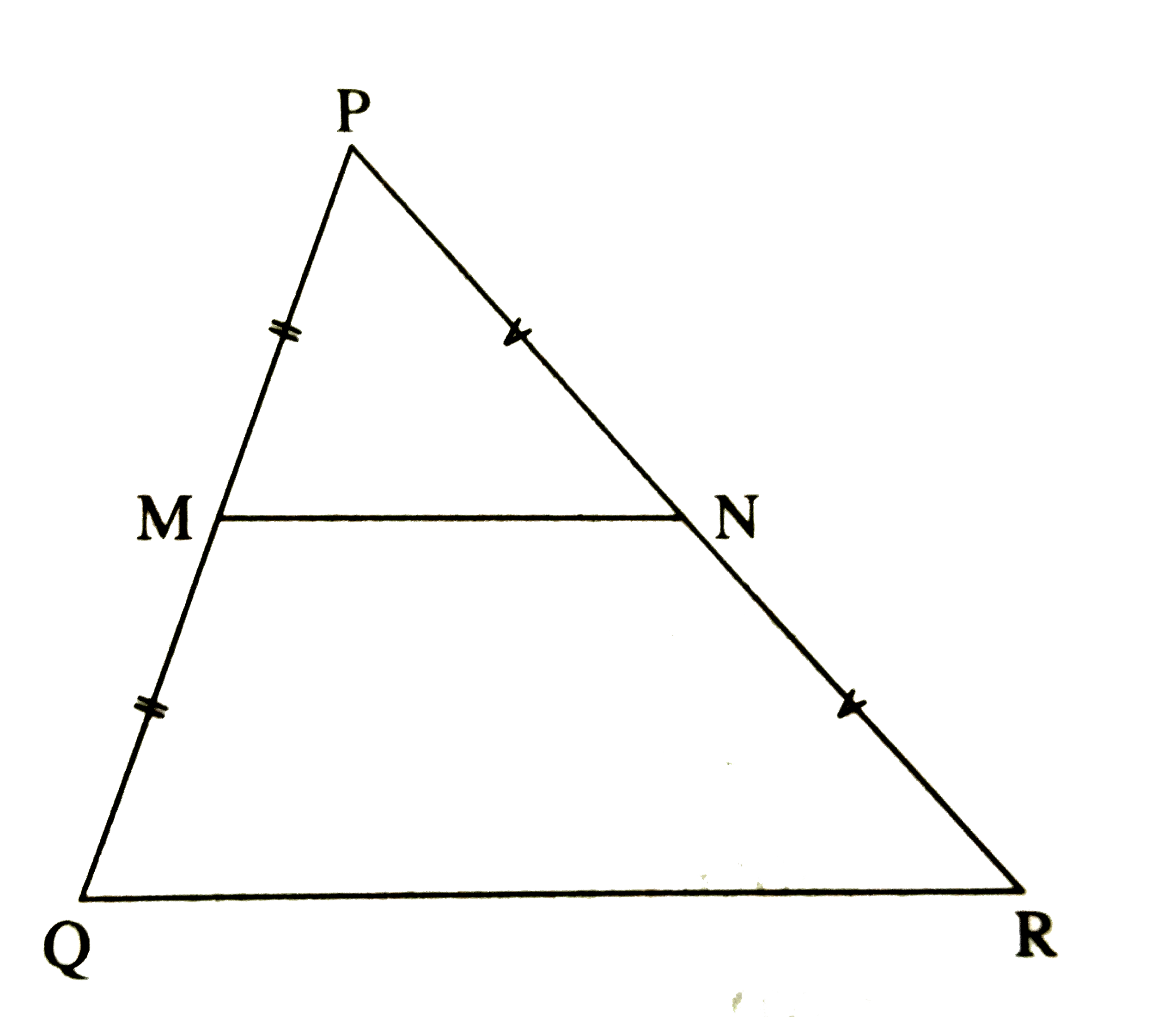
In the figure, M and N are the midpoints of sides PQ and PR respectively . If MN =6 cm then find QR. State your reason .View SolutionThe side of a square is 5 m and the perimeter a rectangle is equal to the perimeter of the square. If the length of the rectangle is 6 m, then find the ratio of the areas of the square and the triangle.
View SolutionIn a square PQRS, X and Y are mid points of sides PS and QR respectively. XY and QS intersect a t O. Find the area of ΔXOS, if PQ = 8 cm.
View SolutionThe radius of a circle is a side of a square. The ratio of the areas of the circle and the square is
View SolutionIn the figure, ABCD is a square. E and Fare midpoints of AD and BC respectively. The ratio of areas of ΔGAB and ΔHAB
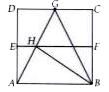 View Solution
View Solution

