Find the value of v :
1012−[812+{7−¯¯¯¯¯¯¯¯¯6−4}]¯¯¯¯¯¯¯¯¯6−4=2 (v)
-3
-2
1
4
The correct Answer is:A
To solve the equation step by step, we will follow the order of operations as per BODMAS/BIDMAS rules, which stands for Brackets, Orders (i.e., powers and roots, etc.), Division and Multiplication (from left to right), Addition and Subtraction (from left to right).
Given equation:
1012−(812+{7−¯(6−4)})¯(6−4)=2v
Step 1: Simplify the bar notation
The bar notation indicates that we should calculate the value inside the bar first. Here, we have:
¯(6−4)=2
So we can replace ¯(6−4) with 2.
Step 2: Substitute the value
Now, substitute 2 into the equation:
1012−(812+{7−2})⋅2=2v
Step 3: Calculate the expression inside the brackets
First, calculate 7−2:
7−2=5
Now substitute this back into the equation:
1012−(812+5)⋅2=2v
Step 4: Calculate the mixed numbers
Convert the mixed numbers to improper fractions:
1012=212
812=172
Step 5: Substitute the improper fractions
Now substitute these values back into the equation:
212−(172+5)⋅2=2v
Step 6: Calculate the expression inside the brackets
Convert 5 to a fraction:
5=102
Now substitute:
212−(172+102)⋅2=2v
Step 7: Combine the fractions
Combine the fractions inside the brackets:
172+102=272
Now substitute this back:
212−(272)⋅2=2v
Step 8: Multiply by 2
Now multiply 272 by 2:
272⋅2=27
So the equation becomes:
212−27=2v
Step 9: Convert 27 to a fraction
Convert 27 to a fraction:
27=542
Now substitute:
212−542=2v
Step 10: Subtract the fractions
Now perform the subtraction:
21−542=2v
−332=2v
Step 11: Divide by 2
Now divide both sides by 2:
v=−334
Final Answer
Thus, the value of v is:
v=−334
1012−(812+{7−¯(6−4)})¯(6−4)=2v
The bar notation indicates that we should calculate the value inside the bar first. Here, we have:
¯(6−4)=2
So we can replace ¯(6−4) with 2.
Now, substitute 2 into the equation:
1012−(812+{7−2})⋅2=2v
First, calculate 7−2:
7−2=5
Now substitute this back into the equation:
1012−(812+5)⋅2=2v
Convert the mixed numbers to improper fractions:
1012=212
812=172
Now substitute these values back into the equation:
212−(172+5)⋅2=2v
Convert 5 to a fraction:
5=102
Now substitute:
212−(172+102)⋅2=2v
Combine the fractions inside the brackets:
172+102=272
Now substitute this back:
212−(272)⋅2=2v
Now multiply 272 by 2:
272⋅2=27
So the equation becomes:
212−27=2v
Convert 27 to a fraction:
27=542
Now substitute:
212−542=2v
Now perform the subtraction:
21−542=2v
−332=2v
Now divide both sides by 2:
v=−334
Thus, the value of v is:
v=−334
Topper's Solved these Questions
- BOOK - MAHENDRACHAPTER - SIMPLIFICATIONEXERCISE - EXERCISE75videos
SIMPLIFICATION
- BOOK - MAHENDRACHAPTER - SIMPLE INTEREST & COMPOUND INTERESTEXERCISE - EXERCISE30videos
SIMPLE INTEREST & COMPOUND INTEREST
- BOOK - MAHENDRACHAPTER - SPEED, TIME AND DISTANCEEXERCISE - EXERCISE25videos
SPEED, TIME AND DISTANCE
Similar Questions
Knowledge Check
- Question 1 - Select One
Find the vlaue of 27×1.¯2×5.526¯2×0.¯6.
A121.¯¯¯¯57B121.¯¯¯¯75C121.7¯5DNone of these - Question 2 - Select One
For any natural number p and q (i) p # q = p 3 + q 3 + 3 and p ∗ q = p 2 + q 2 + 2 and p $ q = | p − q | (ii) Max (p,q) = Maximum of (p,q) and Min (p and q) = Minimum of (p,q)The value of [(1$2)#(3$4)]⋅[(5$6)#(7$8)] is :
A25B52C36Dnone of these
Find the value of 3.¯4×5.¯6
View SolutionFind the value of [(14)2×(17)2]÷[(17)6÷(17)1]
View SolutionWhat is the value of 1.¯¯¯¯34+4.1¯2 ?
View SolutionFind the value of (−8u2v6)×(−20uv) for u=2.5 and v=1
View SolutionFind the value of ( 2.¯6 - 0.¯9 ) is
( a ) 4/3
( b ) 1 /3
( c ) 5/3View Solution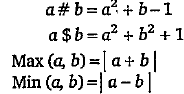
Find the value of Min[(1#2) $ 3, 4#(5$6)] $ Max (6#7), (7#8)] :View Solution

