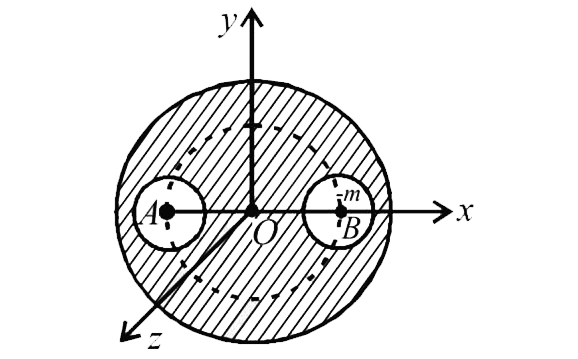
A solid sphere of uniform density and radius 4 units is located with its centre of at the origin O of co
ordinates. Two spheres of equal radii 1 unit with their centres at A(-2,0,0) and B(2,0,0) respectively are taken ou
of the solid leaving behind spherical cavities as shown in figure. Then which of the following statements are true?
(a) The gravitational force due to this object at the origin is zero.
(b) The gravitational force at the point B(2,0,0) is zero.
The gravitational potential is the same at all points on the circle y2+Z2=36
(d) The gravitational potential is the same at all points on the circle y2+Z2=4

Considering the sphere to be made of spheres A and B of radius 1 unit and the remainder R, M=(43)π43P
and MA=MB=(43)πI3p=(M64)
(a) As the force at the centre of a sphere is zero →FA+→FB+→FR=0 and →FB are equal and opposite for
point O, i.e., →FA+→FB=0, so →FR=0, i.e., statement (a) is true.
(b) As the force at a distance r (<R) from the centre of a solid sphere. F=(GMmR3)r so F due to whole sphere
at B will be (GMm43)2. So
→FA+→FB+→FR=(2GMm64)
Howerver, FB=0 as the point B at the centre of sphere B and FA=[G(M/64)m/42] as the point B is
outside it . so
FR=2GMm64−GMm64×16=GMm64[2−116]≠0
i.e., statement (b) is not true.
(C) For a circle y2+z2=36 , the radius of the circle =6 and so the point is outside the sphere and as for external
point V=−(GMr).
VA+VB+VR=−(GM6)
Now as for spheres A and B the distance of the point on the cirlce r=√62+22=√40 and the point is
outside the spheres A and B, so
VA=VB=−G(M/64)√40
∴VR=−GM6−2[−GM64√40]=−GM2
[13−132√10]= constant.
i.e., potential at all points of the circle y2+z2=36 is same, so statement (C) is true.
(d) For a circle y2+z2=4, the radius of the circle =2 and so the point is inside the sphere at a distance (4-2)=
2 units from its centre so
∴V=−GM2R3(3R2−r2)=−GM2×64(48−4)=−22GM64
so VA+VB+VR=−(22GM64)
But as for spheres A and B, the distance of the pont on the cirlce r=√22+22=2√2 and the point
outside the sphere A or B, So VA=VB=−(GM/64)2√2
∴VR=−[22GM64−2GM64×2√2] = −GM64[22−1√2] = constant.
i.e., potential at all points of the cirle y2+z2=4 is same , So statement (d) is true.
Similar Questions
A solid sphere of uniform density and radius 4 units is located with its centre at the origin O of coordinates. Two sphere of equal radii 1 unit, with their centres at A(-2,0 ,0) and B(2,0,0) respectively, are taken out of the solid leaving behind spherical cavities as shown if fig Then:
View SolutionA solid sphere of uniform density and radius 4 units is located with its centre at the origin O of coordinates. Two sphere of equal radii 1 unit, with their centres at A(-2,0 ,0) and B(2,0,0) respectively, are taken out of the solid leaving behind spherical cavities as shown if fig Then:

View Solution
Knowledge Check
A solid sphere of uniform density and radius 4 units is located with its centre at the origin O of coordinates. Two sphere of equal radii 1 unit, with their centres at A(-2,0 ,0) and B(2,0,0) respectively, are taken out of the solid leaving behind spherical cavities as shown if fig Then:
 AThe gravitational force due to this object at the origin is zero.Bthe gravitational force at the point B(2,0,0) is zero.Cthe gravitational potential is the same at all points of circle y2+z2=36Dthe gravitational potential is the same at all points on the circle y2+z2=4.
AThe gravitational force due to this object at the origin is zero.Bthe gravitational force at the point B(2,0,0) is zero.Cthe gravitational potential is the same at all points of circle y2+z2=36Dthe gravitational potential is the same at all points on the circle y2+z2=4.
Statement I: The magnitude of the gravitational potential at the surface of solid sphere is less than that of the centre of sphere. Statement II: Due to the solid sphere, the gravitational potential is the same within the sphere.AStatement I is True, Statement II is True: Statement II is a correct explanation for Statement I.BStatement I is True, Statement II is True: Statement II is Not a correct explanation for Statement I.CStatement I is True, Statement II is False.DStatement I is False, Statement II is True.A spherical hole is made in a solid sphere of radius R. The mass of the sphere before hollowing was M. The gravitational field at the centre of the hole due to the remaining mass is
 AzeroBGM8R2CGM2R2DGMR2
AzeroBGM8R2CGM2R2DGMR2
A solid sphere of uniform density and radius 4 units is located with its centre at the origin O of coordinates. Two sphere of equal radii 1 unit, with their centres at A(-2,0 ,0) and B(2,0,0) respectively, are taken out of the solid leaving behind spherical cavities as shown if fig Then:

The gravitational field due to this object at the orgin is zero.
The gravitational force at point B(2, 0, 0) is zero.
The gravitational force at point B(2, 0, 0) is zero.
Both (1) & (3)
View SolutionA solid sphere of uniform density and radius 4 units is located with its centre at the origin O of coordinates. Two sphere of equal radii 1 unit, with their centres at A(-2,0 ,0) and B(2,0,0) respectively, are taken out of the solid leaving behind spherical cavities as shown if fig Then:

View Solution
Statement I: The magnitude of the gravitational potential at the surface of solid sphere is less than that of the centre of sphere. Statement II: Due to the solid sphere, the gravitational potential is the same within the sphere.
View SolutionA spherical hole is made in a solid sphere of radius R. The mass of the sphere before hollowing was M. The gravitational field at the centre of the hole due to the remaining mass is

View SolutionA hemi-spherical cavity is created in solid sphere (of radius 2R) as shown in the figure. Then

View Solution
