The pressure of gas above the surface of oil in the tank shown in Fig. is (K×105)N/m2. (It is given that the density of oil =800kg/m3, density of mercury=13.6×103kg/m3, atmospheric pressure=103N/m2,g=10m/s2). The value of K to the nearest integer is
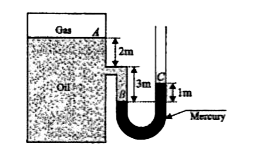
The correct Answer is:2
Let P = pressure of gas (ie, pressure at point A)
Then, PB−PA=ρoil(2+3)=800×10×5=0.4×105N/m2
and PB−PC=ρmercuryg(1)=13.6×103×10×1=1.36×105N/m2
⇒PA−PC=1.36×105−0.4×105=0.96×105N/m2
∴PA=PC+0.96×105=105+0.96×105=1.96×105 =2×105N/m2
Similar Questions
What is the pressure in an ocean at a depth of 1000 m, if the density of water is 1.024×103kgm3. Atmospheric pressure P.=1.01×105 Pa.
View SolutionA tank contains water and mercury as shown in figure. An iron cube of edge d=6 cm is in equilibrium as shown. (density of iron =7.8×103kg/m3, density of mercury =13.6×103kg/m3, density of water =103kgm3)(Neglect the atmospheric pressure)

Time period of small oscillations of block is
View Solution
Knowledge Check
A tank contains water and mercury as shown in figure. An iron cube of edge d=6 cm is in equilibrium as shown. (density of iron =7.8×103kg/m3, density of mercury =13.6×103kg/m3, density of water =103kgm3)(Neglect the atmospheric pressure)

Time period of small oscillations of block isA2π√dρFe(ρHg−ρW)gB2π√dρFe(ρHg+ρW)gC2π√dρFeρHggD2π√dρFeρwg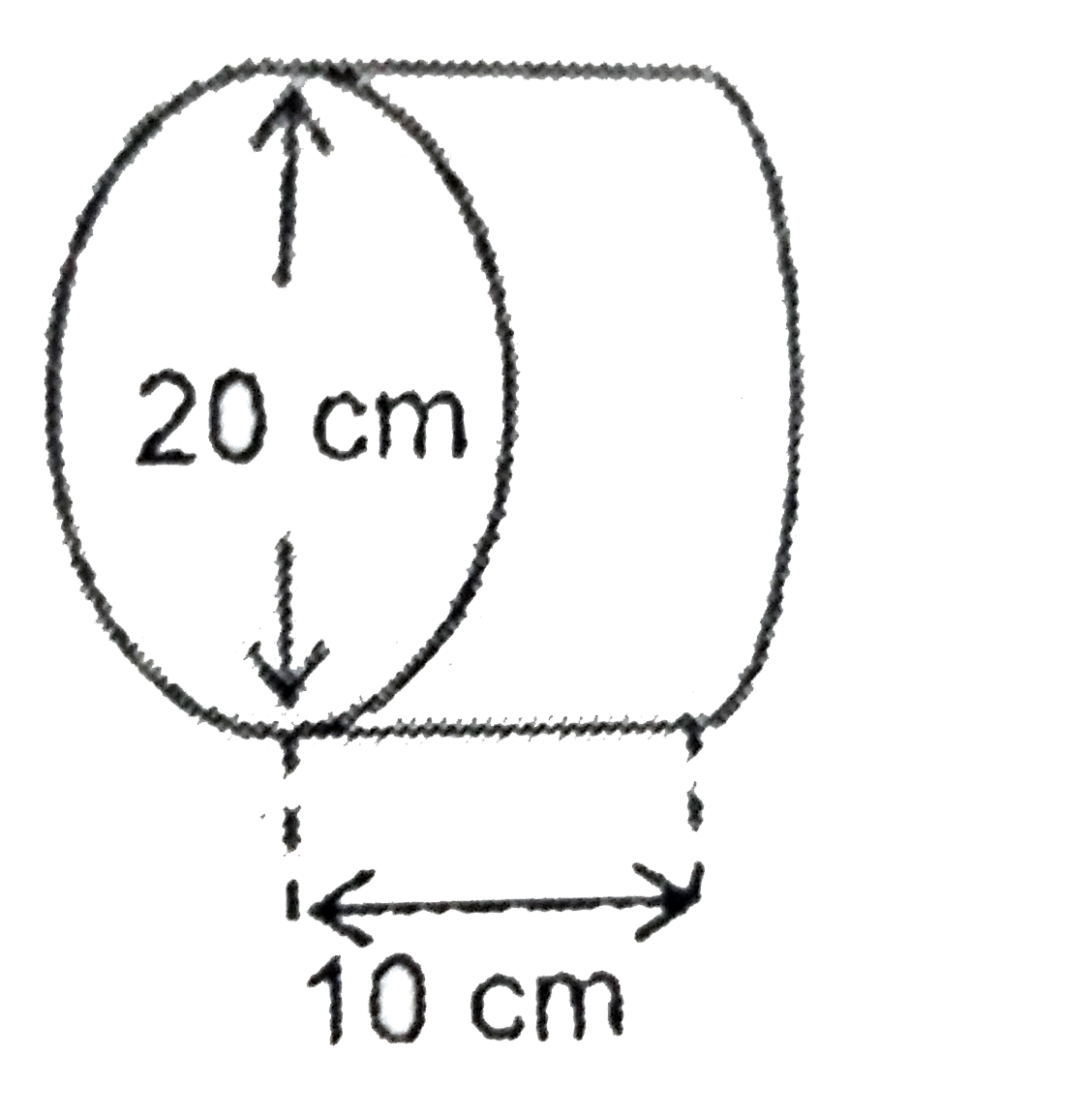
The density of the solid cylindrical bar shown in the figure is5×103 kg m−3 . The weight of the bar is _________ N. (take g=10 m s2A157B1570C320D3.2The heart of a man pumps 5 liters of blood through the arteries per minutes at a pressure of 150 mm of mercury. If the density of mercury by 13.6×103kg/m3 and g=10m/s2 then the power of heart in watt is
A3.0B1.50C1.70D2.35
The bulk modulus of mercury is 2.8×1010 N/m2 and the density is 13600 kg/m2. What is the speed of sound in mercury ?
View Solution76 cm of mercury column is a measure of atmospherice pressure. Express it is N/m2 Given density of mercury is 13.6×103kg/m3
View SolutionThe pressure at a point in water is 10 N/m2. The depth below this point where the pressure becomes double is (Given density of water = 103 kg m−3, g = 10 m s−2)
View SolutionThe pressure at a point in water is 10 N/m2. The depth below this point where the pressure becomes double is (Given density of water = 103 kg m−3, g = 10 m s−2)
View SolutionAt a depth of 500 m in an ocean what is the absolute pressure? Given that the density of seawater is 1.03×103kgm−3 and g=10ms2
View Solution
