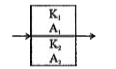
Two plates of same thickness, of coefficients of thermal conductivities $K_{1} and K_{2}$ and areas of cross-section $A_{1} and A_{2}$ are connected as shown, the common coefficient of thermal conductivity K will be:

A

$K_{1} A_{1} + K_{2} A_{2}$

B

$\frac{K_{1} A_{1} + K_{2} A_{2}}{A_{1} + A_{2}}$

C

$\frac{K_{1} A_{2} + K_{2} A_{1}}{A_{1} + A_{2}}$

D

$\frac{K_{1} A_{1}}{K_{2} A_{2}}$

Text Solution

Verified by Experts

The correct Answer is:B

$\frac{d Q}{d t} = \frac{d Q_{1}}{d t} + \frac{d Q_{2}}{d t}$
$\frac{K (A_{1} + A_{2}) (θ_{1} - θ_{2})}{d} = \frac{K_{1} A_{1} (θ_{1} - θ_{2})}{d t} + \frac{K_{2} A_{2} (θ_{1} - θ_{2})}{d} ∴ K = \frac{K_{1} A_{1} + K_{2} A_{2}}{A_{1} + A_{2}}$

Updated on:21/07/2023

|

Class 11 PHYSICS THERMAL EXPANSION AND CALORIMETRY

Similar Questions

Knowledge Check

A wall consists of alternating blocks withlength 'd' and coefficient of thermal conductivity $k_{1}$ and $k_{2}$ . The cross sectional area of the blocks are the same. The equivalent coefficient of thermal conductivity of the wall between left and right is:-

A $K_{1} + K_{2}$
B $\frac{(K_{1} + K_{2})}{2}$
C $\frac{K_{1} K_{2}}{K_{1} + K_{2}}$
D $\frac{2 K_{1} + K_{2}}{K_{1} + K_{2}}$
A wall consists of alternating blocks withlength 'd' and coefficient of thermal conductivity $k_{1}$ and $k_{2}$ . The cross sectional area of the blocks are the same. The equivalent coefficient of thermal conductivity of the wall between left and right is:-

A $K_{1} + K_{2}$
B $\frac{(K_{1} + K_{2})}{2}$
C $\frac{K_{1} + K_{2}}{K_{1} + K_{2}}$
D $\frac{2 K_{1} + K_{2}}{K_{1} + K_{2}}$
A wall consists of alternating blocks withlength 'd' and coefficient of thermal conductivity $k_{1}$ and $k_{2}$ . The cross sectional area of the blocks are the same. The equivalent coefficient of thermal conductivity of the wall between left and right is:-

A $\frac{K_{1} + K_{2}}{2}$
B $\frac{2 K_{1} + K_{2}}{K_{1} + K_{2}}$
C $\frac{K_{1} + K_{2}}{3}$
D $\frac{3 K_{1} + K_{2}}{K_{1} + K_{2}}$

Recommended Questions

Home
Ask Doubt
Profile