The half life of $^{198} A u$ is 2.7 days. Calculate
activity of 2.00 mg of $^{198} A u$ . At.wt.of $^{198} A u = 198$ gm/mol.

Text Solution

Verified by Experts

Activity $= A = λ N$
198 gm of $^{198} A u$ has $6.02 \times 10^{23}$ atom
No. of atoms in 2 mg of Au $= \frac{6.02 \times 10^{23} \times 2 \times 10^{- 3}}{198} = 6.08 \times 10^{18}$
$A = λ N = 2.97 \times 10^{- 6} \times 6.08 \times 10^{18} = 18.06 \times 10^{12}$ dis/sec.
$1 c u = 3.7 \times 10^{10}$ dis/sec
$= \frac{18.06 \times 10^{12}}{3.7 \times 10^{10}} = 4.88 \times 10^{2} = 488 C i$

Class 12 PHYSICS ATOMIC PHYSICS

Knowledge Check

Gold nucleus $(_{79}^{198} A u)$ can decay into mercuyr nucleus $(_{80}^{198} H g^{8})$ by two decay schemes shown in figure below (i) it can emit a $β$ -particle $(β_{1})$ and come to ground state by either emiting one $γ$ - ray ( $γ_{1}$ ) or emitting two $γ$ - rays ( $γ_{3}$ and $γ_{4}$ ) (ii) It can emit one $β$ - particle $(β_{2})$ and come to ground state by emitting $γ_{2}$ ray. Atomic masses: $^{198} A u = 197.9652$ amu and $^{198} H g = 197.9662$ amu. Given that 1 amu= $930 M e V / c^{2}$ . The energy levels of the nucleus are shown in figure below

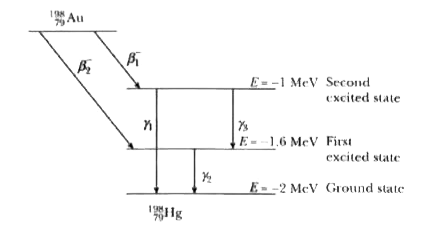
Whatis the maximum kinetic energy of emitted $β_{2}$ particle?
A1.44 MeV
B0.59 MeV
C1.86 MeV
D1.46 MeV
Gold nucleus $(_{79}^{198} A u)$ can decay into mercuyr nucleus $(_{80}^{198} H g^{8})$ by two decay schemes shown in figure below (i) it can emit a $β$ -particle $(β_{1})$ and come to ground state by either emiting one $γ$ - ray ( $γ_{1}$ ) or emitting two $γ$ - rays ( $γ_{3}$ and $γ_{4}$ ) (ii) It can emit one $β$ - particle $(β_{2})$ and come to ground state by emitting $γ_{2}$ ray. Atomic masses: $^{198} A u = 197.9652$ amu and $^{198} H g = 197.9662$ amu. Given that 1 amu= $930 M e V / c^{2}$ . The energy levels of the nucleus are shown in figure below

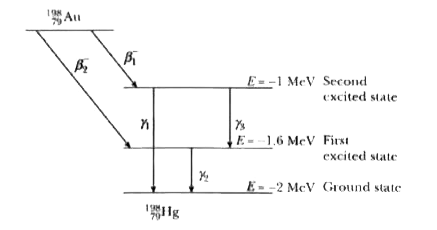
The wavelength of emitted $γ$ - rays is the order
A $λ_{2} > λ_{3} > λ_{1}$
B $λ_{3} > λ_{2} > λ_{1}$
C $λ_{1} > λ_{2} > λ_{3}$
D $λ_{3} = λ_{2} = λ_{1}$
Gold nucleus $(_{79}^{198} A u)$ can decay into mercuyr nucleus $(_{80}^{198} H g^{8})$ by two decay schemes shown in figure below (i) it can emit a $β$ -particle $(β_{1})$ and come to ground state by either emiting one $γ$ - ray ( $γ_{1}$ ) or emitting two $γ$ - rays ( $γ_{3}$ and $γ_{4}$ ) (ii) It can emit one $β$ - particle $(β_{2})$ and come to ground state by emitting $γ_{2}$ ray. Atomic masses: $^{198} A u = 197.9652$ amu and $^{198} H g = 197.9662$ amu. Given that 1 amu= $930 M e V / c^{2}$ . The energy levels of the nucleus are shown in figure below

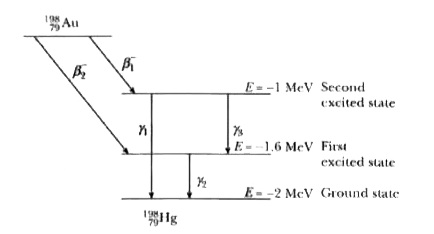
What is the maximum kinetic energy of emitted $β_{1}$ parricle ?
A1.28 MeV
B0.77 MeV
C1.86 MeV
D0.86 MeV

The half life of $^{198} A u$ is 2.7 days. Calculate
activity of 2.00 mg of $^{198} A u$ . At.wt.of $^{198} A u = 198$ gm/mol.

Similar Questions

Knowledge Check

Recommended Questions

The half life of 198Au is 2.7 days. Calculate activity of 2.00 mg of 198Au . At.wt.of 198Au=198 gm/mol.

Activity =A=λN 198 gm of 198Au has 6.02×1023 atom No. of atoms in 2 mg of Au =6.02×1023×2×10−3198=6.08×1018 A=λN=2.97×10−6×6.08×1018=18.06×1012 dis/sec. 1cu=3.7×1010 dis/sec =18.06×10123.7×1010=4.88×102=488Ci

Similar Questions

Knowledge Check

Recommended Questions

The half life of $^{198} A u$ is 2.7 days. Calculate
activity of 2.00 mg of $^{198} A u$ . At.wt.of $^{198} A u = 198$ gm/mol.