PQ is a common chord of two circles. APB is a secant line joining points A and B on the two circles. Two tangents AC and BC are drawn. If ∠ACB=45∘, then what is ∠AQB equal to ?
75∘
90∘
120∘
135∘
To solve the problem step by step, we will use the properties of tangents and angles in circles.
Step 1: Understand the Configuration
We have two circles with a common chord PQ. A secant line APB intersects the circles at points A and B. Tangents AC and BC are drawn from point A and point B respectively. We know that angle ACB = 45°.
Hint: Visualize the circles and the points A, B, C, and P. This will help you understand the relationships between the angles.
Step 2: Use the Tangent Properties
Since AC and BC are tangents from the same external point A and B, we know that:
- AC = BC (tangents from a point to a circle are equal).
Hint: Recall that tangents drawn from an external point to a circle are equal in length.
Step 3: Set Up the Angles in Triangle ACB
In triangle ACB, we have:
- Angle ACB = 45°
- Let angle CAB = angle CBA = x (since AC = BC, the angles opposite to equal sides are equal).
Using the triangle angle sum property:
CAB+ACB+CBA=180°
This gives us:
x+45°+x=180°
So:
2x+45°=180°
Hint: Remember that the sum of angles in a triangle is always 180°.
Step 4: Solve for x
Rearranging the equation:
2x=180°−45°
2x=135°
x=135°2=67.5°
Hint: Simplifying the equation step by step will help you find x easily.
Step 5: Apply the Alternate Segment Theorem
According to the alternate segment theorem:
- Angle CAB (which is x) is equal to angle AQP.
- Angle CBA (which is also x) is equal to angle BQP.
Thus:
- AQP = 67.5°
- BQP = 67.5°
Hint: The alternate segment theorem states that the angle between a tangent and a chord is equal to the angle in the alternate segment.
Step 6: Find Angle AQB
Now, angle AQB can be found by adding angles AQP and BQP:
AQB=AQP+BQP
AQB=67.5°+67.5°=135°
Hint: When finding the angle at a point, sum the angles that meet at that point.
Final Answer
Thus, the measure of angle AQB is:
135°
We have two circles with a common chord PQ. A secant line APB intersects the circles at points A and B. Tangents AC and BC are drawn from point A and point B respectively. We know that angle ACB = 45°.
Since AC and BC are tangents from the same external point A and B, we know that:
- AC = BC (tangents from a point to a circle are equal).
In triangle ACB, we have:
- Angle ACB = 45°
- Let angle CAB = angle CBA = x (since AC = BC, the angles opposite to equal sides are equal).
CAB+ACB+CBA=180°
This gives us:
x+45°+x=180°
So:
2x+45°=180°
Rearranging the equation:
2x=180°−45°
2x=135°
x=135°2=67.5°
According to the alternate segment theorem:
- Angle CAB (which is x) is equal to angle AQP.
- Angle CBA (which is also x) is equal to angle BQP.
- AQP = 67.5°
- BQP = 67.5°
Now, angle AQB can be found by adding angles AQP and BQP:
AQB=AQP+BQP
AQB=67.5°+67.5°=135°
Thus, the measure of angle AQB is:
135°
Similar Questions
Knowledge Check
- Question 1 - Select One
From a point P outside the circle with centre O, two tangents PA and PB are drawn to meet the circle at A and B respectively. If ∠APB=70∘, then ∠OAB is equal to :
केंद्र O वाले वृत्त के बाहर स्थित किसी बिंदु P से दो स्पर्श रेखाएं PA और PB खींची जाती हैं जो वृत्त से क्रमशः A और B मिलती हैं | यदि ∠APB=70∘ है, तो कोण OAB का मान ज्ञात करें |A35∘B65∘C45∘D55∘ - Question 2 - Select One
AC and BC are two equal chords of a circle. BA is produced to any point P and CP, when joined cuts the circle at T. Then
ACT:TP=AB:CABCT:TP=CA:ABCCT:CB=CA:CPDCT:CB=CP:CA - Question 3 - Select One
PA and PB are two tangents to a circle with centre O, from a point P outside the circle. A and B are points on the circle. If ∠APB=40∘, then ∠OABis equal to:
A40∘B20∘C50∘D25∘
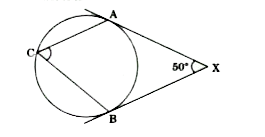
In the figure given below, XA and XB are two tangents to a circle. If ∠AXB=50∘ and AC is parallel to XB, then what is ∠ACB equal to ?
 View Solution
View SolutionIf from any point on the common chord of two intersecting circles, tangents be drawn to the circles, prove that they are equal.
View SolutionA chord PQ of a circle is parallel to the tangent drawn at a point R of the circle,Prove that R bisects the arc PRQ.
View SolutionTwo circles touch each other externally at point P. A common tangent AB is drawn touching the circles at A and B. Find ∠APB.
View SolutionT is a point on the common tangents at P of two circles and if TA and TB are respectively the other tangents at A and B to the two circles drawn from the point T then
View Solution

