Consider the following statements :
Statement-I: Let PQR be a triangle in which PQ = 3 cm, QR = 4 cm and RP = 5 cm. If D is a point in the plane of the triangle PQR such that D is either outside it or inside it, then
DP+DQ+DR>6cm.
Statement-II : PQR is a right-angled triangle. Which one of the following is correct in respect of the above two statements ?
Both statement-I and statement-II are individually true and statement-II is the correct explanation of statement-I.
Both statement-I and statement-II are individually true and statement-II is not the correct explanation of statement-I.
Statement-I is true and statement-II is false.
Statement-I is false and statement-II is true.
To solve the problem, we need to analyze the two statements regarding triangle PQR and point D.
Step 1: Verify if Triangle PQR is a Right-Angled Triangle
Given:
- PQ=3cm
- QR=4cm
- RP=5cm
We can use the Pythagorean theorem to check if triangle PQR is a right-angled triangle. According to the theorem, if c is the longest side (hypotenuse), then:
c2=a2+b2
Here, we have:
- c=RP=5cm
- a=PQ=3cm
- b=QR=4cm
Calculating:
RP2=52=25
PQ2+QR2=32+42=9+16=25
Since RP2=PQ2+QR2, we conclude that triangle PQR is indeed a right-angled triangle.
Step 2: Analyze Statement I
Statement I claims that for any point D in the plane of triangle PQR (either inside or outside), the sum DP+DQ+DR>6cm.
Using the triangle inequality property:
1. In triangle DPQ:
DP+DQ>PQ⇒DP+DQ>3
2. In triangle DQR:
DQ+DR>QR⇒DQ+DR>4
3. In triangle DPR:
DP+DR>RP⇒DP+DR>5
Step 3: Combine Inequalities
Adding the three inequalities:
(DP+DQ)+(DQ+DR)+(DP+DR)>3+4+5
This simplifies to:
2DP+2DQ+2DR>12
Dividing by 2:
DP+DQ+DR>6
Thus, Statement I is true.
Step 4: Conclusion on Statements
- Statement I is true.
- Statement II is also true since we have verified that triangle PQR is a right-angled triangle.
However, there is no direct relation between the two statements, meaning that while both are true, Statement II does not explain Statement I.
Final Answer
Both statements are true, but Statement II is not the correct explanation of Statement I.
---
Given:
- PQ=3cm
- QR=4cm
- RP=5cm
- c=RP=5cm
- a=PQ=3cm
- b=QR=4cm
RP2=52=25
PQ2+QR2=32+42=9+16=25
Statement I claims that for any point D in the plane of triangle PQR (either inside or outside), the sum DP+DQ+DR>6cm.
1. In triangle DPQ:
DP+DQ>PQ⇒DP+DQ>3
2. In triangle DQR:
DQ+DR>QR⇒DQ+DR>4
3. In triangle DPR:
DP+DR>RP⇒DP+DR>5
Adding the three inequalities:
(DP+DQ)+(DQ+DR)+(DP+DR)>3+4+5
This simplifies to:
2DP+2DQ+2DR>12
Dividing by 2:
DP+DQ+DR>6
- Statement I is true.
- Statement II is also true since we have verified that triangle PQR is a right-angled triangle.
Both statements are true, but Statement II is not the correct explanation of Statement I.
Similar Questions
Knowledge Check
- Question 1 - Select One
PQRSis a rectangle in which side of PQ=24cm. and QR=16cm. T is a point on RS. What is the area (in cm.) of the triangle PTQ?
A192B162C148DCannot be determined - Question 2 - Select One
In a triangle PQR, PQ = 20 cm and PR = 6 cm, the side QR is :
Aequal to 14 cmBless than 14 cmCgreater than 14 cmDnone of these - Question 3 - Select One
In ΔPQR,PQ=4 cm, PR = 6 cm and QR = 3 cm . Which of the following is correct ?
A∠R>∠QB∠Q>∠RC∠Q=∠RD∠R<∠P
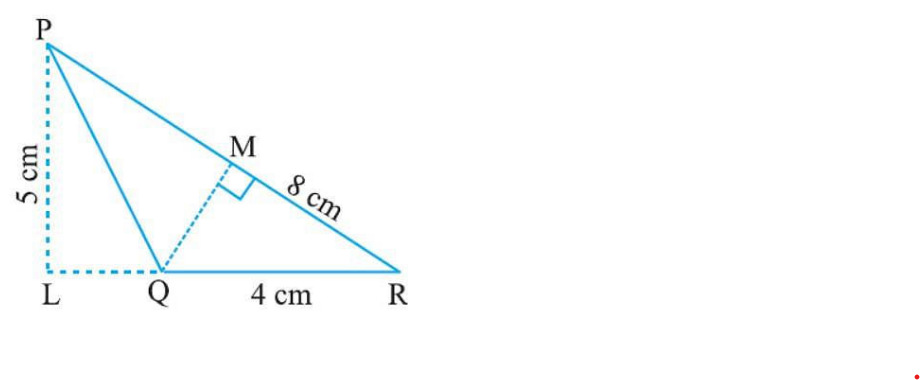
In ΔPQR,PR=8cm,QR=4cmandPL=5cm (Fig 11.22). Find: (i) the area of the ΔPQR (ii) QM
 View Solution
View SolutionIn the triangle PQR, C is the centroid. PQ = 30 cm, QR = 36 cm and PR = 50 cm. If D si the midpoint of QR, then what is the length (in cm) of CD?
View SolutionIn △PQR,PQ=10 cm , QR =12 , PR =8 cm . Find out the greatest and the smallest angle of the triangle .
View SolutionConstruct a triangle PQR in which QR = 6cm, ∠Q=60∘ and PR – PQ = 2cm.
View SolutionIn ΔPQR,PQ=4cm,PR=6cmandQR=3cm. Which of the following is correct?
View Solution

