A circle circumscribes a rectangle with sides 16cm and 12cm. What is the area of the circle
48π square cm
50π square cm
100π square cm
200π square cm
To find the area of the circle that circumscribes a rectangle with sides 16 cm and 12 cm, we can follow these steps:
Step 1: Identify the sides of the rectangle
The sides of the rectangle are given as:
- Length (l) = 16 cm
- Breadth (b) = 12 cm
Step 2: Calculate the diagonal of the rectangle
The diagonal of the rectangle can be calculated using the Pythagorean theorem. The formula for the diagonal (d) is:
d=√l2+b2
Substituting the values:
d=√162+122
d=√256+144
d=√400
d=20 cm
Step 3: Determine the radius of the circumscribed circle
The diagonal of the rectangle is the diameter of the circumscribed circle. Therefore, the radius (r) is half of the diameter:
r=d2
r=202
r=10 cm
Step 4: Calculate the area of the circle
The area (A) of the circle can be calculated using the formula:
A=πr2
Substituting the radius:
A=π(10)2
A=π(100)
A=100π cm2
Final Answer
The area of the circle is 100π cm2.
---
The sides of the rectangle are given as:
- Length (l) = 16 cm
- Breadth (b) = 12 cm
The diagonal of the rectangle can be calculated using the Pythagorean theorem. The formula for the diagonal (d) is:
d=√l2+b2
d=√162+122
d=√256+144
d=√400
d=20 cm
The diagonal of the rectangle is the diameter of the circumscribed circle. Therefore, the radius (r) is half of the diameter:
r=d2
r=202
r=10 cm
The area (A) of the circle can be calculated using the formula:
A=πr2
A=π(10)2
A=π(100)
A=100π cm2
The area of the circle is 100π cm2.
Similar Questions
A circle is drawn circumscribing a rectangle of sides 24 cm and 7 cm. Find the area of the circle. (Take π=3.14)
एक वृत्त 24 cm और 7 cm भुजा वाले आयत के परिगत है। वृत्त का क्षेत्रफल ज्ञात कीजिए।( π=3.14)
View SolutionFind the difference in the area of a circle circumscribed about a regular hexagon with sides of 10 cm and the area of the circle inscribed inside the same hexagon.
View Solution
Knowledge Check
A circle circumscribes a rectangle whose sides are in the ratio of 4 :3 If the area of the rectangle is 192cm2, then the perimeter (in cm) of the circle is :
A20πB10πC12πD15πA circle and a rectangle have the same perimeter.The sides of the rectangle are 18 cm and 26 cm. What is the area of the circle ?
A88cm2B154cm2C616cm2D1250cm2A circle is circumscribed by the rhombus which in turn is made up by joining the mid-points of a rectangle whose sides, 12 cm and16 cm respectively. What is the area of the circle ?
A62526πB67625πC57625πDcan't be determined
Find the area of the shaded region in the given figure, if ABCD is a rectangle with sides 8 cm and 6 cm and O is the centre of the circle.
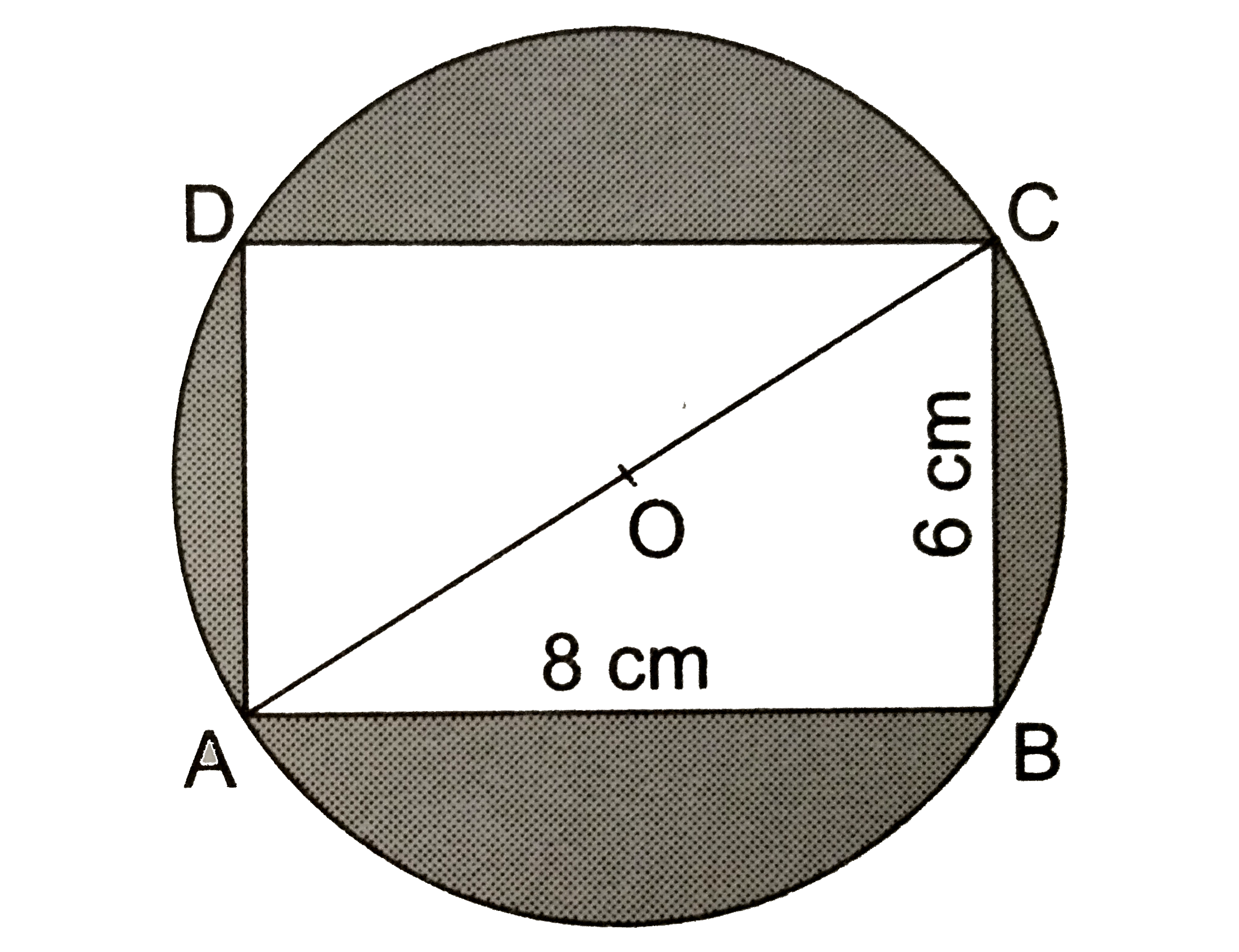
View SolutionA circle and a rectangle have the same perimeter. The sides of the rectangle are 18 cm and 26 cm. What is the area of the circle? (a) 88 cm2 (b) 154 cm2 (c) 1250 cm2 (d) Cannot be determined (e) None of these
View SolutionA circle has been drawn around a rectangle of sides 6 cm and 8 cm, then find the area of the region inside the circle and outside the rectangle.
View SolutionFind the area of circle in the figure, if ABCD is a rectangle with sides 8 cm and 6 cm and O is the centre of circle. (Take π = 3.14)

View SolutionA circle is circumscribed by the rhombus which in turn is made up by joining the mid points of a rectangle whose sides, 12 cm. and 16 cm. respectively. What is the area of the circle?
View Solution
