From a certain point on a straight road, a person observes a tower in the west direction at a distance of 200 m. He walks some distance 'along the road and finds that the same tower is 300 m south of him. What is the shortest distance of the tower from the road?
300√13 m
500√13 m
600√13 m
900√13 m
To solve the problem step by step, we will first visualize the situation and then apply trigonometric relationships to find the shortest distance of the tower from the road.
Step 1: Visualize the Situation
- Let point O be the initial position of the person on the road.
- The tower is located 200 m to the west of point O. We can denote this point as T.
- The person walks along the road and reaches point A, where the tower is now observed to be 300 m to the south.
Step 2: Set Up the Coordinates
- We can set the coordinates as follows:
- Point O (0, 0)
- Point T (−200, 0) (200 m west of O)
- Point A (0, y) where y is the distance the person walked along the road.
Step 3: Determine the Position of Point A
- According to the problem, the tower (point T) is now 300 m south of point A.
- Therefore, the coordinates of point T can also be expressed as (0, y - 300).
Step 4: Establish the Relationship
- From the coordinates, we can set up the equation based on the y-coordinates:
- The y-coordinate of T is 0 (since it is on the horizontal line of the road).
- The y-coordinate of A is y, and the tower is 300 m south of A, which gives us:
y−300=0⟹y=300
Step 5: Calculate the Distance from the Road
- The shortest distance from the tower to the road is the horizontal distance from point T to the vertical line of the road (which is the x-axis).
- The distance from point T (−200, 0) to the road (y = 0) is simply the x-coordinate of T, which is 200 m.
Step 6: Conclusion
- The shortest distance of the tower from the road is 200 m.
Final Answer
The shortest distance of the tower from the road is 200 m.
- Let point O be the initial position of the person on the road.
- The tower is located 200 m to the west of point O. We can denote this point as T.
- The person walks along the road and reaches point A, where the tower is now observed to be 300 m to the south.
- We can set the coordinates as follows:
- Point O (0, 0)
- Point T (−200, 0) (200 m west of O)
- Point A (0, y) where y is the distance the person walked along the road.
- According to the problem, the tower (point T) is now 300 m south of point A.
- Therefore, the coordinates of point T can also be expressed as (0, y - 300).
- From the coordinates, we can set up the equation based on the y-coordinates:
- The y-coordinate of T is 0 (since it is on the horizontal line of the road).
- The y-coordinate of A is y, and the tower is 300 m south of A, which gives us:
y−300=0⟹y=300
- The shortest distance from the tower to the road is the horizontal distance from point T to the vertical line of the road (which is the x-axis).
- The distance from point T (−200, 0) to the road (y = 0) is simply the x-coordinate of T, which is 200 m.
- The shortest distance of the tower from the road is 200 m.
The shortest distance of the tower from the road is 200 m.
Similar Questions
Knowledge Check
A car is travelling on a straight road leading to a tower. From a point at a distance of 500 m from the tower, as seen by the driver, the angle of elevation of the top of the tower is 30∘. After driving towards the tower for 10 seconds, the angle of elevation of the top of the tower as seen by the driver is found to be 60∘. Then the speed of the car is
A135 km/hrB110 km/hrC120 km/hrD90 km/hrA man standing at a point P is watching the top of elevation of 30∘. The man walks some distance towards the tower and then his angle of elevation of thetop of the toweris 60∘. If the height of the tower 30 m, then the distance he moves is
A20 mB20 V 3 mC22 mD22 V3 mIf the angle of depression of an object from a 75 m high tower is 30∘, then the distance of the object from the tower is
A25√3 mB50√3 mC75√3 mD150 m
Suppose angle of depression from top of the tower to point A is 45∘ and height of tower is 10 m. What is the distance of point A from the building?
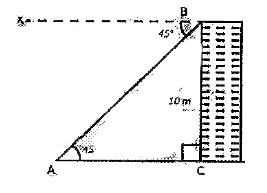
View SolutionA tower stands near an airport. The angle of elevation θ of the tower from a point on the ground such that its tangent is 512. Find the height of the tower, if the distance of the observer from the tower is 120m.
View SolutionFrom a point on the ground which is at a distance of 50 m from the foot of the towe, the angle of elevation of the top of the tower is observed to be 30∘. Find the height of the tower.
View SolutionA tower of height 15 m stands vertically on the ground. From a point on the ground the angle of elevation of the top of the tower is found to be 30∘. What is the distance of the point from the foot of the tower?
View SolutionTwo observers are stationed due north of a tower at a distance of 20 m from each other. If the elevations of the tower observed by them are 30∘and45∘ respectively, then the height of the tower is
View Solution
