If ' s are the midpoints of the class intervals of grouped data, 's are the corresponding frequencies and is the mean, then what is equal to ?
0
-1
1
2
To solve the problem, we need to analyze the expression given and use the properties of the mean in grouped data.
1. Understand the Mean Formula:
The mean (¯x) of grouped data is calculated using the formula:
¯x=Σ(fixi)n
where fi are the frequencies, xi are the midpoints of the class intervals, and n is the total number of observations.
2. Manipulate the Mean Formula:
Rearranging the mean formula gives us:
Σ(fixi)=n¯x
3. Substitute into the Given Expression:
The expression we need to evaluate is:
Σ(fixi)−¯x
We can substitute n¯x for Σ(fixi):
Σ(fixi)−¯x=n¯x−¯x
4. Factor Out ¯x:
This simplifies to:
n¯x−¯x=¯x(n−1)
5. Evaluate the Expression:
Since we are looking for Σ(fixi)−¯x, we can see that this expression is not equal to zero unless n=1. However, the question asks for Σ(fixi)−n¯x:
Σ(fixi)−n¯x=0
Thus, the expression simplifies to:
Σ(fixi)−n¯x=0
6. Final Conclusion:
Therefore, we conclude that:
Σ(fixi)−¯x=0
Final Answer:
Σ(fixi)−¯x=0
The mean (¯x) of grouped data is calculated using the formula:
¯x=Σ(fixi)n
where fi are the frequencies, xi are the midpoints of the class intervals, and n is the total number of observations.
Rearranging the mean formula gives us:
Σ(fixi)=n¯x
The expression we need to evaluate is:
Σ(fixi)−¯x
We can substitute n¯x for Σ(fixi):
Σ(fixi)−¯x=n¯x−¯x
This simplifies to:
n¯x−¯x=¯x(n−1)
Since we are looking for Σ(fixi)−¯x, we can see that this expression is not equal to zero unless n=1. However, the question asks for Σ(fixi)−n¯x:
Σ(fixi)−n¯x=0
Thus, the expression simplifies to:
Σ(fixi)−n¯x=0
Therefore, we conclude that:
Σ(fixi)−¯x=0
Σ(fixi)−¯x=0
Similar Questions
If ¯x=1nn∑i=1xi then prove that n∑i=1(xi−¯x)=0
View SolutionThe measurments ( in mm) of the diameters of the head of the screws are given below :
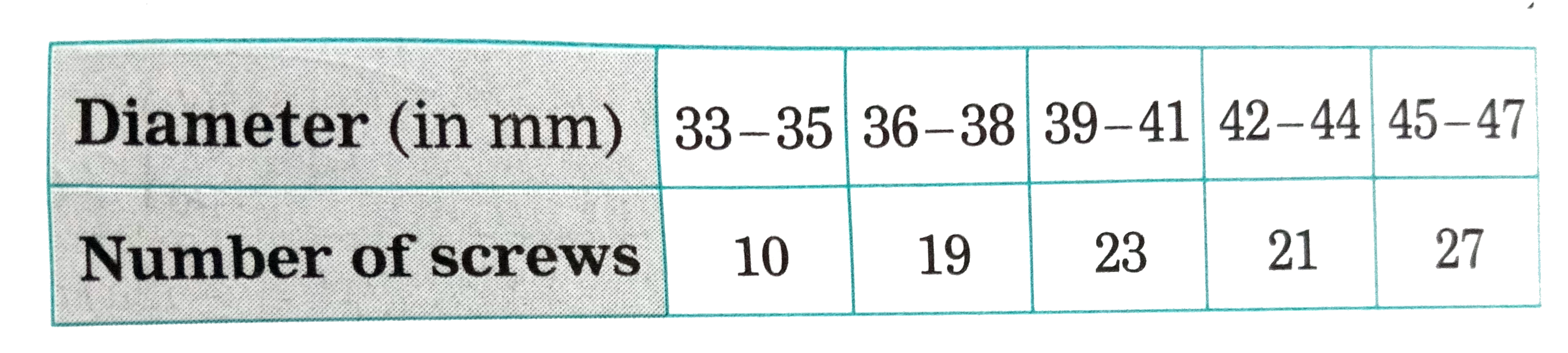
Calculate the mean diameter of the screw by ' Assumed Mean Method' .
Steps to calculate mean by this method :
(1) Assume mean A. In this example , A = 40. (Generally, the class mark of the class having the maximum frequency or the class mark of the middle class is chosen as the assumed mean.)
(2) In column 1, write the class intervals,(Here, diameter).
(3) In column 2, write the corresponding class marks.
(4) In column 3, write the value of di, where di=xi−A.
A is the assumed mean.
(5) In column 4, write the frequencies (fi). Write Σfi at the bottom of this column.
(6) In column 5, write the product (fi×di) and their sum Σfidi.
Calculate ¯d and ¯¯¯X using the following formulae :
¯d=ΣfidiΣfi. Mean¯¯¯X=A+¯d.
[d : mean of deviations.]
View Solution
Knowledge Check
If xi's are the mid-points of the class intervals of grouped data, fi's are the corresponding frequencies and ¯x is the mean, then ∑(fixi−¯x) equal to
A0B−1C1D2If xi's are the mid-points of the class intervals of grouped data fi's are the corresponding frequencies and x is the mea, then ∑(fixi−x) is equal to
A0B−1C1D2If xi' is the mid-points of the class intervals of grouped data, fi' s are corresponding frequencies and ¯x is the mean , then find the value of ∑(fixi−¯x).
A0B1C2D3
Mean of a frequency distribution (¯x) is 45. If Σfi=20 find Σfixi
View SolutionIf ¯x is the mean of x1,x2,…,xn then the value of n∑i=1(xi−¯x) is
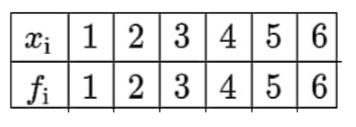
View SolutionLet xi represents the outcome on a fair die and fi be the corresponding frequency. The variance for random variable di with following frequency distribution, is
View SolutionIf ¯x is the mean of x1,x2,x3,.....,xn, then n∑i=1(xi−¯x)=
View SolutionThe algebraic sum of the deviations of xifi from the mean is:
View Solution
