A pipe with square cross-section is supplying water to a cistern which was initially empty. The area of cross-section is 4 cm² and the nozzle velocity of water is 40 m/s. The dimensions of the cistern are 10 m x 8 m x 6 m. Then the cistern will be full in
9.5 hours
9 hours
8 hours 20 minutes
8 hours
To solve the problem, we need to determine how long it will take to fill the cistern with water from the pipe. We can follow these steps:
1. Identify the dimensions of the cistern:
The dimensions of the cistern are given as:
- Length (L) = 10 m
- Width (W) = 8 m
- Height (H) = 6 m
2. Calculate the volume of the cistern:
The volume (V) of the cistern can be calculated using the formula:
V=L×W×H
Substituting the values:
V=10m×8m×6m=480m3
3. Convert the volume from cubic meters to cubic centimeters:
Since the area of the cross-section of the pipe is given in cm², we need to convert the volume of the cistern into cubic centimeters:
1m3=106cm3
Therefore,
V=480m3×106cm3/m3=480×106cm3
4. Determine the area of the cross-section of the pipe:
The area of the cross-section of the pipe is given as:
A=4cm2
5. Determine the velocity of water through the nozzle:
The nozzle velocity of water is given as:
v=40m/s
6. Calculate the volume of water flowing per second:
The volume flow rate (Q) can be calculated using the formula:
Q=A×v
Substituting the values (note that we need to convert the velocity from m/s to cm/s):
v=40m/s=4000cm/s
Therefore,
Q=4cm2×4000cm/s=16000cm3/s
7. Calculate the time required to fill the cistern:
The time (t) required to fill the cistern can be calculated using the formula:
t=Volume of cisternVolume flow rate
Substituting the values:
t=480×106cm316000cm3/s=30000s
8. Convert time from seconds to hours and minutes:
To convert seconds into hours, we divide by 3600:
t=30000s3600s/h≈8.33hours
This can be expressed as:
8hours20minutes
Final Answer:
The cistern will be full in approximately 8 hours and 20 minutes.
The dimensions of the cistern are given as:
- Length (L) = 10 m
- Width (W) = 8 m
- Height (H) = 6 m
The volume (V) of the cistern can be calculated using the formula:
V=L×W×H
Substituting the values:
V=10m×8m×6m=480m3
Since the area of the cross-section of the pipe is given in cm², we need to convert the volume of the cistern into cubic centimeters:
1m3=106cm3
Therefore,
V=480m3×106cm3/m3=480×106cm3
The area of the cross-section of the pipe is given as:
A=4cm2
The nozzle velocity of water is given as:
v=40m/s
The volume flow rate (Q) can be calculated using the formula:
Q=A×v
Substituting the values (note that we need to convert the velocity from m/s to cm/s):
v=40m/s=4000cm/s
Therefore,
Q=4cm2×4000cm/s=16000cm3/s
The time (t) required to fill the cistern can be calculated using the formula:
t=Volume of cisternVolume flow rate
Substituting the values:
t=480×106cm316000cm3/s=30000s
To convert seconds into hours, we divide by 3600:
t=30000s3600s/h≈8.33hours
This can be expressed as:
8hours20minutes
The cistern will be full in approximately 8 hours and 20 minutes.
Similar Questions
A pipe of varying area of cross-section is held such that its axis is horizontal. At two cross sections A and B, its radii are 8 cm and 4 cm. If velocity of water at A through the pipe is 16 cm s−1 and pressure at A is 10−6 dyne/cm2 , find the pressure at cross-section B.
View SolutionWater flowing steadily through a horizontal pipe of non-unifrom cross-section. If the pressure of water is 4×104N/m2 at a point where cross-section is 0.02m2 and velocity of flow is 2ms−1 . The pressure at a point where cross-section reduces to 0.01m2 is 3.4×10n Pa. What is the value of n ?
View Solution
Knowledge Check
- Question 1 - Select One
In the previous question, at the mouth of the tap the area of cross-section is 2.5cm2 and the speed of water in 3m/s. The area of cross-section of the water column 80cm below the tap is.
A2cm2B1.5cm2C1cm2D0.5cm2 - Question 2 - Select One
At the mount of the tap area of cross-section is 2.0cm2 and the speed of water is 3m/s. The area of cross-section of the water column 80 cm below the tap is (use g=10m/s2)
A0.6cm2B1.2cm2C1.5cm2D2.0cm2 - Question 3 - Select One
The cross-section of a canal is in the shape of a trapezium and the area of cross-section is 360m2. If the canal is 12 m wide at the top and 8 m wide at the bottom the depth of the canal is :
A36 cmB180 cmC45 cmDnone of these
Water is flowing steadily through a horizontal pipe of non-uniform cross-section. If the pressure of water is 4×104N/m2 at a point where cross-section is 0.02m2 and velocity of flow is 2m/s. What is the pressure at a point where cross-section reduces to 0.01m2 ?
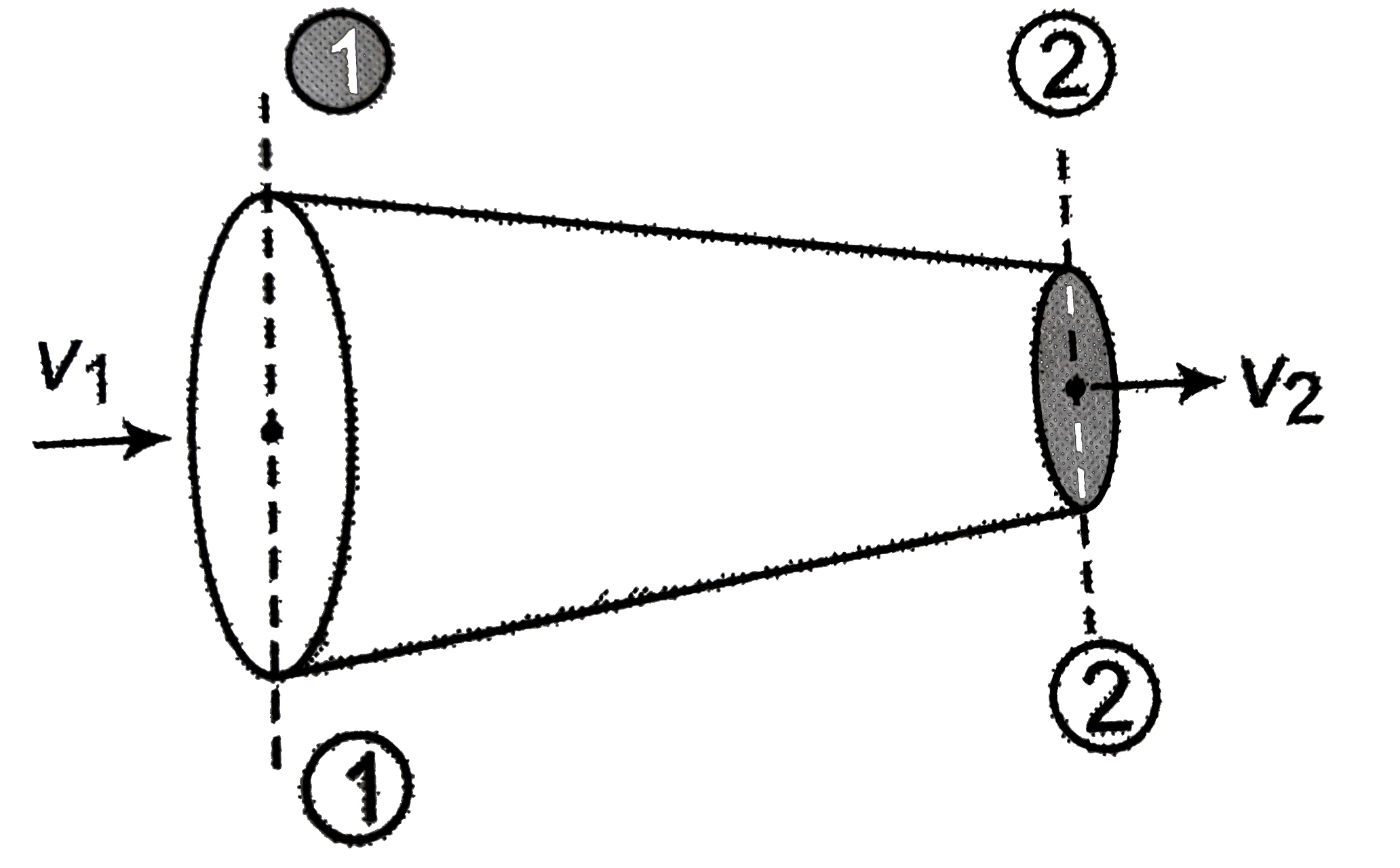 .View Solution
.View SolutionThe cross-section of a canal is in the shape of a trapezium and the area of cross-section is 360m2. If the canal is 12 m wide at the top and 8 m wide at the bottom the depth of the canal is :
View SolutionA horizontal pipe of cross-section diameter 5cm carries water at a speed of 4ms−1. The pipe is connected to a smaller pipe with a cross-sectional diameter 4cm. The velocity of water through the smaller pipe is
View SolutionA horizontal pipe of cross sectional diameter 5 cm carries water at a velocity of 4m/s. The pipe is connected to a smaller pipe with a cross-sectional diameter 4 cm. The velocity of water through the smaller pipe is:
View SolutionA horizontal pipe of cross sectional diameter 5 cm carries water at a velocity of 4m/s. The pipe is connected to a smaller pipe with a cross-sectional diameter 4 cm. The velocity of water through the smaller pipe is:
View Solution

