From the solid gold in the form of a cube of side length 1 cm, spherical solid balls each having the surface area π1/3cm2 are to be made. Assuming that there is no loss of the material in the process of making the balls, the maximum number of balls made will be
3
4
6
9
To solve the problem step by step, we will follow the outlined process:
Step 1: Calculate the Volume of the Cube
The volume V of a cube is given by the formula:
V=side3
Given that the side length of the cube is 1 cm, we have:
V=13=1 cm3
Hint: Remember that the volume of a cube is calculated by raising the length of one side to the power of three.
Step 2: Determine the Surface Area of a Sphere
The surface area A of a sphere is given by the formula:
A=4πr2
We are given that the surface area of each spherical ball is π1/3 cm². Setting the two equal gives:
4πr2=π1/3
Hint: To find the radius, isolate r2 in the surface area formula.
Step 3: Solve for the Radius r
Dividing both sides by π:
4r2=π1/3π=π−2/3
Now, solving for r2:
r2=π−2/34=14π2/3
Taking the square root to find r:
r=12π−1/3
Hint: When solving for r, remember to take the square root of both sides after isolating r2.
Step 4: Calculate the Volume of a Single Sphere
The volume Vs of a sphere is given by:
Vs=43πr3
Substituting r:
Vs=43π(12π−1/3)3
Calculating r3:
r3=(12)3(π−1/3)3=18π−1
Now substituting back into the volume formula:
Vs=43π⋅18⋅1π=424=16 cm3
Hint: Make sure to cube the radius correctly and simplify the expression.
Step 5: Calculate the Maximum Number of Balls
To find the maximum number of spherical balls that can be made from the cube, divide the volume of the cube by the volume of one sphere:
Number of balls=Volume of the cubeVolume of one sphere=1 cm316 cm3=6
Hint: When dividing volumes, ensure you are dividing the total volume by the volume of a single unit to find the total number of units.
Conclusion
The maximum number of spherical solid balls that can be made from the solid gold cube is 6.
Final Answer: 6
The volume V of a cube is given by the formula:
V=side3
Given that the side length of the cube is 1 cm, we have:
V=13=1 cm3
The surface area A of a sphere is given by the formula:
A=4πr2
We are given that the surface area of each spherical ball is π1/3 cm². Setting the two equal gives:
4πr2=π1/3
Dividing both sides by π:
4r2=π1/3π=π−2/3
Now, solving for r2:
r2=π−2/34=14π2/3
Taking the square root to find r:
r=12π−1/3
The volume Vs of a sphere is given by:
Vs=43πr3
Substituting r:
Vs=43π(12π−1/3)3
Calculating r3:
r3=(12)3(π−1/3)3=18π−1
Now substituting back into the volume formula:
Vs=43π⋅18⋅1π=424=16 cm3
To find the maximum number of spherical balls that can be made from the cube, divide the volume of the cube by the volume of one sphere:
Number of balls=Volume of the cubeVolume of one sphere=1 cm316 cm3=6
The maximum number of spherical solid balls that can be made from the solid gold cube is 6.
Similar Questions
By melting three spherical solid balls of radius 1 cm, 2 cm and 3 cm, respectively, a large spherical ball is formed. If 25% material is lost in this process, what will be the radius of the new ball?
View SolutionHow many cubes of side 2 cm can be made from a solid cube of side 10 cm ?
View Solution
Knowledge Check
Three spherical balls of radius 3 cm, 2 cm and 1 cm are melted to form a new spherical ball. In this prcoess there is a loss of 25% of the material. What is the radius (in cm) of the new ball ?
A5B3C6D8Three spherical balls of radius 2 cm, 4 cm and 6 cm are melted to form a new spherical ball. In this process there is a loss of 25% of the material. What is the radius (in cm) of the new ball?
A6B8C12D16The solid as shown in the figure, is made up of cubical blocks each of side 1 cm. The number of blocks is
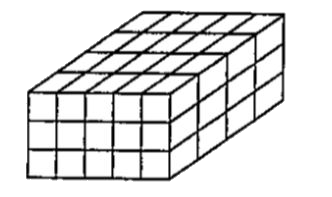 A52B60C72D48
A52B60C72D48
How many cubes of side 5 cm can be made from a solid cube of side 10 cm ?
View SolutionAn iron solid sphere of radius 3cm is melted and recast into small sperical balls ofradius 1cm each. Assuming that there is no wastage in the process, find the number ofsmall spherical balls made from the given sphere.in order to reach the destination
View SolutionA solid metal ball of radius 8 cm is melted and cast into smaller balls, each of radius 2 cm. The number of balls made are ……….. .
View SolutionThree cubes each of sides 7 cm are joined end to end. Find the surface area of the resulting solid.
View SolutionA solid metal ball of diameter 16 cm is melted and cast into smaller balls, each of radius 1 cm. The number of such balls is :
View Solution
