Suppose chords AB and CD of a circle intersect at a point P inside the circle. Two right-angled triangles A'P'B' and C'Q'D' are formed as shown in the figures below such that A'P' = AP, B'P' = BP, C'Q' = CP, D'Q' = DP and ∠A'P'B'=90∘=∠C'O'D':
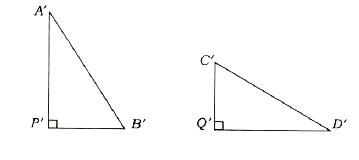
Which of the following statements are not correct?
1. A'P'B' and C'O'D' are similar triangles, but need not be congruent.
2. A'P'B' and C'Q'D' are congruent triangles.
3. A'P'B' and C'Q'D' are triangles of same area.
4. A'P'B' and C'Q'D' are triangles of same perimeter.
Select the correct answer using the code given below.
2 and 3 only
1 and 3 only
1, 2 and 4 only
1, 2, 3 and 4
Step by step video & image solution for Suppose chords AB and CD of a circle intersect at a point P inside the circle. Two right-angled triangles A'P'B' and C'Q'D' are formed as shown in the figures below such that A'P' = AP, B'P' = BP, C'Q' = CP, D'Q' = DP and angleA'P'B' = 90^(@) = angleC'O'D': Which of the following statements are not correct? 1. A'P'B' and C'O'D' are similar triangles, but need not be congruent. 2. A'P'B' and C'Q'D' are congruent triangles. 3. A'P'B' and C'Q'D' are triangles of same area. 4. A'P'B' and C'Q'D' are triangles of same perimeter. Select the correct answer using the code given below. by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Updated on:21/07/2023Similar Questions
In Figure two chords AB and CD of a circle intersect each other at the point P (when produced) outside the circle. Prove that
(i) ΔPAC~ΔPDB
(ii) PA.PB=PC.PD

View SolutionTwo circles intersect each other at the points P and Q. Two straight lines through P and Q intersect one circle at the points A and C and the other circle at B and D. Prove the AC|| BD
View Solution
Knowledge Check
Two circles with centres P and Q intersect at B and C, A, D are points on the circles with centres P and Q respectively such that A, C, D are colliner. If ∠APB=130∘,and∠BQD=x∘, then the value of x is :
A65B130C195D135Two circles with centres P and Q intersect at B and C, A, D are points on the circles with centres P and Q respectively such that A, C, D are colliner. If ∠APB=130∘,and∠BQD=x∘, then the value of x is :
A65B130C195D135The tangents at two points A and B on the circle with centre O intersect at P. If in quadrilateral PAOB, ∠AOB:∠APB=5:1, then measure of ∠APB is :
A30∘B60∘C45∘D15∘
In Figure, AB and CD are two chords of a circle, intersecting each other at P such that AP=CP. Show that AB=CD
View SolutionIn the figure, two chords AB and CD intersect each other at the point P.
Prove that : AP. PB = CP. DP

View SolutionLet AB and CD are two parallel chords of circle whose radius is 5 units. If P and Q are mid points of AB and CD respectively such that PA.PB=9,QC.QD=16, then distance betweẹn AB and CD is
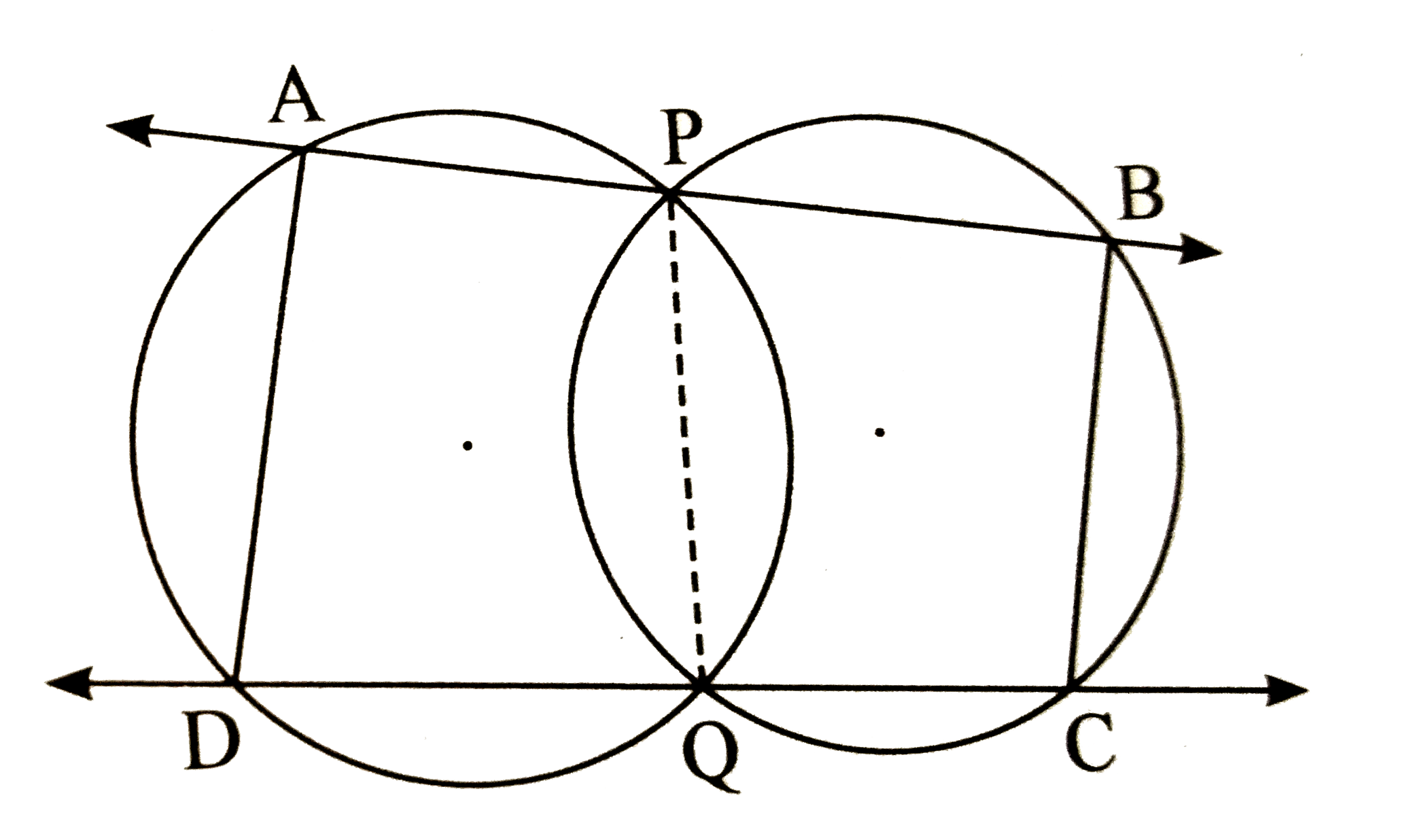
View SolutionTwo circles intersect each other at point P and Q. Secants drawn through p and Q intersect the circles at points A,B and D,C
Prove that :∠ADC+∠BCD=180∘
View SolutionIf ABC≅PQR and ABC is not congruent to RPQ, then which of the following not true: BC=PQ (b) AC=PR (c) AB=PQ (D) QR=BC
View Solution
