A circle and a square have the same perimeter. Which one of the following is correct ?
Their areas are equal
The area of the circle is larger
The area of the square is π2 times area of circle
The area of the square is it times area of circle
To solve the problem, we need to compare the areas of a circle and a square that have the same perimeter. Here’s a step-by-step solution:
Step 1: Define the Perimeter of the Square
Let the side length of the square be a. The perimeter P of the square is given by:
P=4a
Step 2: Define the Perimeter of the Circle
Let the radius of the circle be r. The perimeter (circumference) C of the circle is given by:
C=2πr
Step 3: Set the Perimeters Equal
Since the problem states that the square and the circle have the same perimeter, we can set the two expressions for perimeter equal to each other:
4a=2πr
Step 4: Solve for the Radius r
To find r in terms of a, we can rearrange the equation:
r=4a2π=2aπ
Step 5: Calculate the Area of the Square
The area As of the square is given by:
As=a2
Step 6: Calculate the Area of the Circle
The area Ac of the circle is given by:
Ac=πr2
Substituting r=2aπ into the area formula:
Ac=π(2aπ)2=π⋅4a2π2=4a2π
Step 7: Compare the Areas
Now we need to compare the areas As and Ac:
As=a2andAc=4a2π
To compare these, we can look at the ratio:
AcAs=4a2πa2=4π
Since π is approximately 3.14, we have:
4π>1
This implies:
Ac>As
Conclusion
The area of the circle is greater than the area of the square when both have the same perimeter.
---
Let the side length of the square be a. The perimeter P of the square is given by:
P=4a
Let the radius of the circle be r. The perimeter (circumference) C of the circle is given by:
C=2πr
Since the problem states that the square and the circle have the same perimeter, we can set the two expressions for perimeter equal to each other:
4a=2πr
To find r in terms of a, we can rearrange the equation:
r=4a2π=2aπ
The area As of the square is given by:
As=a2
The area Ac of the circle is given by:
Ac=πr2
Substituting r=2aπ into the area formula:
Ac=π(2aπ)2=π⋅4a2π2=4a2π
Now we need to compare the areas As and Ac:
As=a2andAc=4a2π
To compare these, we can look at the ratio:
AcAs=4a2πa2=4π
Since π is approximately 3.14, we have:
4π>1
This implies:
Ac>As
The area of the circle is greater than the area of the square when both have the same perimeter.
Similar Questions
Knowledge Check
If A and B are commuting square matrices of the same order, then which of the following is/are correct ?
AA and Bn commute, n∈NBAn and B commute, n∈NCA−λ and B+μ commute, λ,μ∈RDA+λ and B−μ commute,λ,μ∈RA circle and a rectangle have the same perimeter.The sides of the rectangle are 18 cm and 26 cm. What is the area of the circle ?
A88cm2B154cm2C616cm2D1250cm2A circle and a rectangle have the same perimeter. The sides of the rectangle are 18 cm and 26 cm. The area of the circle is
[Take π=227]A125cm2B230cm2C550cm2D616cm2
A square, a circle and an equilateral triangle have same perimeter. Consider the following statements :
1. The area of square is greater than the area of the triangle.
2. The area of circle is less than the area of triangle .
Which of the statements is/are correct ?
View SolutionA rectangle and a square have the same perimeter (Fig. 6.10).
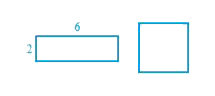
(a) The area of the rectangle is……...
(b) The area of the square is………..
View SolutionA parallelogram and a rectangle stand on the same base and on the same side of the base with the same height. If l1,l2 be the perimeters of the parallelogram and the rectangle respectively, then which one of the following is correct ?
View SolutionA square, a circle and equilateral triangle have same perimeter. Consider the following statements. I. The area of square is greater than the area of the triangle. II. The area of circle is less than the area of triangle. Which of the statement is/are correct?
View SolutionIf A and B are square matrics of the same order then which one of the following is always true ?
View Solution
