त्रिज्या R की एक अचालक चकती है पृष्ठ पर आवेश Q एकसमान रूप से विचरित है चकती कोणीय वेग ω से इसके तल के लम्बवत तथा केंद्र से गुजरने वाली अक्ष के परितः घूर्णन करती है इस घूर्णन के परिणामस्वरूप चकती के केंद्र पर चुम्बकीय क्षेत्र B प्राप्त होता है यदि इस चकती पर रखे गये आवेश तथा इसके कोणीय वेग की नियत रखे तथा चकती को त्रिज्या में परिवर्तन करे तो चकती के केंद्र पर चुम्बकीय क्षेत्र का वितरण कस चित्र द्वारा दशा्रया जाएगा?
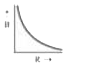
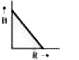
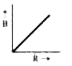

The correct Answer is:A
चकती के आवेश का पृष्ठ घनत्व σ=QπR2
माना चकती अनेक वलयों से निर्मित है एक वलय की त्रिज्या =
r तथा मोटाई =dr है पर आवेश की मात्रा dQ=2πrdrs
वलय के केंद्र पर चुम्बकीय क्षेत्र dB=μ0i2r=μ0dR2rdt
=μ02r(2πrdrσ)×ω2π=μ0σω2dr
∴B=∫R0μ0σω2dr=μ0ω2×RπR2×R
=μ0Rω2πR
या B∝1R
Similar Questions
माना एक दीर्घवृत्त जिसका दीर्घ -अक्ष, X-अक्ष के अनुदिश है तथा केन्द्र मूलबिंदु पर है, के नाभिलम्ब की लम्बाई 8 है । यदि दीर्घवृत्त की नाभियो के बीच की दुरी, इसके लघु-अक्ष की लम्बाई के समान हो, तो निम्न में से कौन-सा बिन्दु इस पर स्थित है?
View Solutionयदि एक अतिपरवलय के शीर्ष (−2,0) तथा (2,0) पर है तथा इसकी एक नाभि (−3,0) पर है, तो निम्न में से कौन-सा बिन्दु इस अतिपरवलय पर स्थित नहीं है
View Solutionयदि R त्रिज्या का एक वृत्त मूलबिंदु O से होकर जाता है तथा निर्देशांक अक्षो को A और B पर कट्टा है , तो O से रेखा AB पर डाले गए लम्ब के पाद का बिन्दुपथ है
View Solutionएक अतिपरवलय बिन्दुओं (3,2) तथा (-17,12) से गुजरता है और उसका केंद्र मूलबिन्दु पर है तथा अनुप्रस्थ अक्ष x- अक्ष है। अतिपरवलय की अनुप्रस्थ अक्ष की लम्बाई है।
View Solutionएक द्विध्रुव 10 सेमी लम्बा तथा आवेश 500μC से बना है। इसके अक्ष से 25 सेमी दूरी पर विद्युत क्षेत्र की तीव्रता होगी
View Solutionयदि वृत्त के केंद्र से 3 सेमी. की दूरी पर स्थित जीवा की लम्बाई 8 सेमी. है, तो वृत्त की त्रिज्या ज्ञात कीजिए।
View Solutionकॉलम - I में कुछ निश्चित स्थितियां दी गई है जिनमे प्रतिरोध का सीधा धात्विक तार प्रयुक्त किया है तथा कॉलम - II में कुछ परिणामी प्रभाव दिए है कॉलम - I के कथनो को कॉलम - II के कथनो से सुलमित कीजिए
कॉलम - I कॉलम - II(A)एक आवेशित संधारित्र को तार के सिरों से जोड़ा गया है(p) एक नियत धारा तार में से प्रवाहित होती है(B)तार को इसकी लम्बाई के लम्बवत नियत वेग से एक समान चुम्बकीय क्षेत्र में गतिमान किया जाता है चुम्बकीय क्षेत्र गति के तल के लम्बवत है(q)उष्मीय ऊर्जा तार में उत्पन्न होती है(C)तार को नियत विधुत क्षेत्र में रखा जाता है जिसकी दिशा तार की लम्बाई के अनुदिश है(r)तार के सिरों पर एक नियत विभवान्तर उत्पन्न होता है(D)तार के सिरों पर एक नियत वि. वा. बल. की बैट्री जोड़ी जाती है(s)तार के सिरों का नियत परिमाण का आवेश उपस्थित होता है
View Solutionवृत्ताकार पथ पर आवेश की गति के कारण केंद्र पर चुंबकीय क्षेत्र|धारावाहि चाप के कारण केंद्र पर चुंबकीय क्षेत्र
View Solution
