Charge Q is given to a spherical conductor of radius R. It is surrounded by a concentric conducting shell of inner radius a and outer radius b. Corresponding electric field diagram will be:




To solve the problem regarding the electric field diagram corresponding to a charge Q given to a spherical conductor of radius R surrounded by a concentric conducting shell with inner radius a and outer radius b, we can follow these steps:
1. Understanding the System:
- We have a spherical conductor with radius R that carries a charge Q.
- This conductor is surrounded by a concentric conducting shell with an inner radius a and an outer radius b.
2. Charge Distribution:
- Since the spherical conductor is a conductor, the charge Q will reside on its surface. Therefore, the surface of the spherical conductor will have a uniform charge distribution.
3. Induced Charge on the Shell:
- The presence of the charge Q on the inner spherical conductor will induce a charge on the inner surface of the conducting shell. According to Gauss's law, the inner surface of the shell will acquire a charge of −Q to maintain electrostatic equilibrium.
- Consequently, the outer surface of the shell will have a charge of +Q (since the shell is neutral overall).
4. Electric Field in Different Regions:
- Region 1 (Inside the conductor, r<R): The electric field E=0 because the electric field inside a conductor in electrostatic equilibrium is zero.
- Region 2 (Between the conductor and the shell, R<r<a): Here, the electric field can be calculated using Gauss's law. The electric field E is directed outward and is given by:
E=14πϵ0⋅Qr2
- Region 3 (Inside the shell, a<r<b): The electric field E=0 because the electric field inside a conductor is zero.
- Region 4 (Outside the shell, r>b): The electric field is again directed outward and can be calculated as:
E=14πϵ0⋅Qr2
5. Electric Field Diagram:
- The electric field lines will be directed outward from the spherical conductor in the region between the conductor and the shell, and will also be directed outward in the region outside the shell.
- Inside the conductor and inside the shell, the electric field is zero.
Conclusion:
The electric field diagram will show:
- No electric field inside the conductor and the shell.
- Outward electric field lines in the region between the conductor and the shell, and also in the region outside the shell.
- We have a spherical conductor with radius R that carries a charge Q.
- This conductor is surrounded by a concentric conducting shell with an inner radius a and an outer radius b.
- Since the spherical conductor is a conductor, the charge Q will reside on its surface. Therefore, the surface of the spherical conductor will have a uniform charge distribution.
- The presence of the charge Q on the inner spherical conductor will induce a charge on the inner surface of the conducting shell. According to Gauss's law, the inner surface of the shell will acquire a charge of −Q to maintain electrostatic equilibrium.
- Consequently, the outer surface of the shell will have a charge of +Q (since the shell is neutral overall).
- Region 1 (Inside the conductor, r<R): The electric field E=0 because the electric field inside a conductor in electrostatic equilibrium is zero.
- Region 2 (Between the conductor and the shell, R<r<a): Here, the electric field can be calculated using Gauss's law. The electric field E is directed outward and is given by:
E=14πϵ0⋅Qr2
- Region 3 (Inside the shell, a<r<b): The electric field E=0 because the electric field inside a conductor is zero.
- Region 4 (Outside the shell, r>b): The electric field is again directed outward and can be calculated as:
E=14πϵ0⋅Qr2
- The electric field lines will be directed outward from the spherical conductor in the region between the conductor and the shell, and will also be directed outward in the region outside the shell.
- Inside the conductor and inside the shell, the electric field is zero.
The electric field diagram will show:
- No electric field inside the conductor and the shell.
- Outward electric field lines in the region between the conductor and the shell, and also in the region outside the shell.
Topper's Solved these Questions
- JEE MAIN 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2021EXERCISE - SECTION-A
80 Videos
- JEE MAIN 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2021EXERCISE - SECTION-B
40 Videos
- JEE MAINBOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINEXERCISE - All Questions
473 Videos
- JEE MAIN 2022BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2022EXERCISE - Question
492 Videos
Similar Questions
Find the capacitance of an isolated spherical conductor of radius a surrounded by a concentric layer of dielectric of outer radius b and relative permittivity. ε
View SolutionA point charge +Q is placed at the centre of an uncharged spherical conducting shell of inner radius a and outer radius b.
i. Find the electric field for r<a.
ii. What is the magnitude and sigh of the induced charge q' on the inner shell surface?
iii. What is the electric field at points r>b?
iv. What id the surface charge on the outer surface of the conductor?
View Solution
Knowledge Check
A solid conducting sphere of radius a having a charge q is surrounded by a concentric conducting spherical shell of inner radius 2a and outer radius 3a as shown in figure. Find the amount of heat porduced when switch is closed (k=14πε0)
 Akq22aBkq23aCkq24aDkq26a
Akq22aBkq23aCkq24aDkq26aA and C are concentric conducting spherical shells of radius a and c respectively.A is sueeounded by a concentric dielectric medium of inner radius a, outer radius b and dielectric constant k. If sphere A is given a charge Q, the potential at the outer surface of the dielectric is
 AQ4πesplion0kbBQ4πε01a+(10k(b−a))C(Q094πε0b)Dnone of these
AQ4πesplion0kbBQ4πε01a+(10k(b−a))C(Q094πε0b)Dnone of theseA hollow conducting sphere of inner radius r and outer radius 2R is given charge Q as shown in figure, then the
 Apotential at A and B is same.Bpotential at O and B is same.Cpotential at O and C is same.Dpotential at A,B,C and O is same.
Apotential at A and B is same.Bpotential at O and B is same.Cpotential at O and C is same.Dpotential at A,B,C and O is same.
A solid spherical conductor has charge +Q and radius R. It is surrounded by a solid spherical shell with charge -Q, innerradius 2R, and outer radius 3R. Which of the following statements is true?
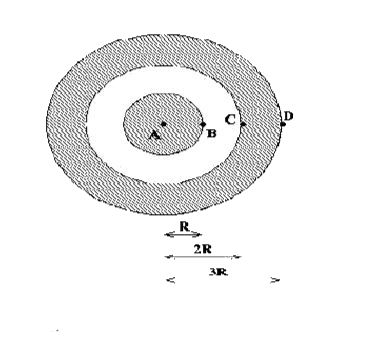
View SolutionA solid conducting sphere of radius R is surrounded by a concentric metallic shell of inner radius 2R and outer radius 3R. The shell is earthed. The inner sphere is connected to a switch S by a thin conducting wire through a small hole in the shell. By closing the switch S, the inner sphere is connected to a distant conducting sphere of radius R having charge Q. Find the charge that flows to earth through wire AB.
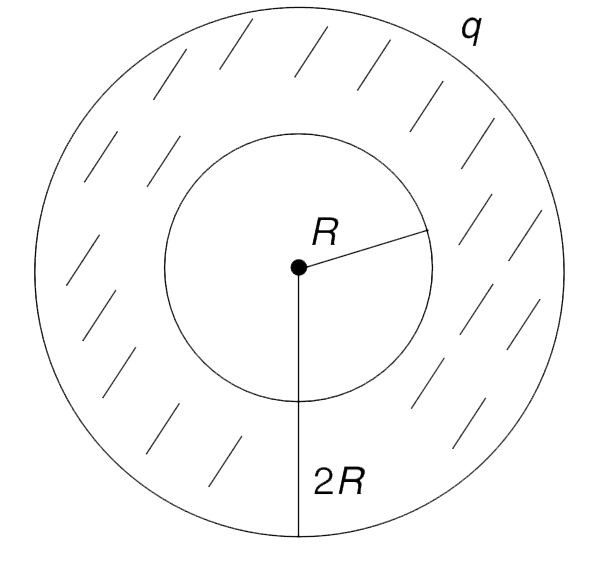
View SolutionA solid conducting sphere of radius R is surrounded by a concentric metallic shell of inner radius 2R and outer radius 3R. The shell is earthed. The inner sphere is connected to a switch S by a thin conducting wire through a small hole in the shell. By closing the switch S, the inner sphere is connected to a distant conducting sphere of radius R having charge Q. Find the charge that flows to earth through wire AB.

View SolutionA spherical conducting shell of radius r0 carry a charge q0. Then value of electric field inside it is :-
View SolutionA nonconducting sphere with radius a is concentric with and surrounded by a conducting spherical shell with inner radius b and outer radius c. The inner sphere has a negative charge uniformly distributed throughout its volume, while the spherical shell has no net charge. The potential V (r) as a function of distance from the center is given by

View Solution
