The area of △ABC is 88cm2. If D is the midpoint of BC and E is the midpoint of AB, then the area (in cm2) of △BDE is:
44
22
11
5.5
The correct Answer is:C
To find the area of triangle BDE given that the area of triangle ABC is 88 cm², we can follow these steps:
Step 1: Understand the Midpoints
Let D be the midpoint of side BC and E be the midpoint of side AB in triangle ABC. This means that BD = DC and AE = EB.
Step 2: Use the Properties of Similar Triangles
Since D and E are midpoints, triangle BDE is similar to triangle ABC. The ratio of their corresponding sides will be 1:2 because the lengths of the segments created by the midpoints are half of the lengths of the sides of triangle ABC.
Step 3: Calculate the Area Ratio
The area of similar triangles is proportional to the square of the ratio of their corresponding sides. Therefore, if the ratio of the sides is 1:2, the ratio of the areas will be:
(12)2=14
Step 4: Apply the Area Ratio to Find Area of Triangle BDE
Let the area of triangle BDE be A_BDE. Then, using the area ratio:
ABDEAABC=14
Given that the area of triangle ABC is 88 cm², we can set up the equation:
ABDE88=14
Step 5: Solve for A_BDE
To find A_BDE, multiply both sides by 88:
ABDE=88×14=22 cm2
Conclusion
Thus, the area of triangle BDE is 22 cm².
---
Let D be the midpoint of side BC and E be the midpoint of side AB in triangle ABC. This means that BD = DC and AE = EB.
Since D and E are midpoints, triangle BDE is similar to triangle ABC. The ratio of their corresponding sides will be 1:2 because the lengths of the segments created by the midpoints are half of the lengths of the sides of triangle ABC.
The area of similar triangles is proportional to the square of the ratio of their corresponding sides. Therefore, if the ratio of the sides is 1:2, the ratio of the areas will be:
(12)2=14
Let the area of triangle BDE be A_BDE. Then, using the area ratio:
ABDEAABC=14
Given that the area of triangle ABC is 88 cm², we can set up the equation:
ABDE88=14
To find A_BDE, multiply both sides by 88:
ABDE=88×14=22 cm2
Thus, the area of triangle BDE is 22 cm².
Similar Questions
The area of △ABC is 44 cm2. If D is the midpoint of BC and E is the midpoint of AB, then the area (in cm2) of △BDE is:
△ABC का क्षेत्रफल 44 वर्ग सेमी है | यदि D, BC का मध्य बिंदु है तथा E, AB का मध्य बिंदु है, तो △BDE का क्षेत्रफल ( वर्ग सेमी में ) होगा :View SolutionABC is a triangle in which D is the midpoint of BC and E is the midpoint of AD.
Prove that ar(△BED)=14ar(△ABC).
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
The area of △ABC is 88cm2. If D is the midpoint of BC and E is the midpoint of AB, then the area (in cm2) of △BDE is:
A44B22C11D5.5 - Question 2 - Select One
The area of ΔABC is 44 cm2 . If D is the midpoint of BC and E is the midpoint of AB, then the area ( in cm2) of ΔBDE is :
A5.5B22C11D44 - Question 3 - Select One
In △ABC, if D is the midpoint of BC and E is the midpoint of AD then ar(△BED) = ?
 A12ar(△ABC)B13ar(△ABC)C14ar(△ABC)D23ar(△ABC)
A12ar(△ABC)B13ar(△ABC)C14ar(△ABC)D23ar(△ABC)
In an equilateral ΔABC,D is the midpoint of AB and E is the midpoint of AC. Then, ar(ΔABC):ar(ΔADE)=?
 View Solution
View SolutionD is the midpoint of side BC of △ABC and E is the midpoint of BD. If O is the midpoint of AE,
prove that ar(△BOE)=18ar(△ABC).
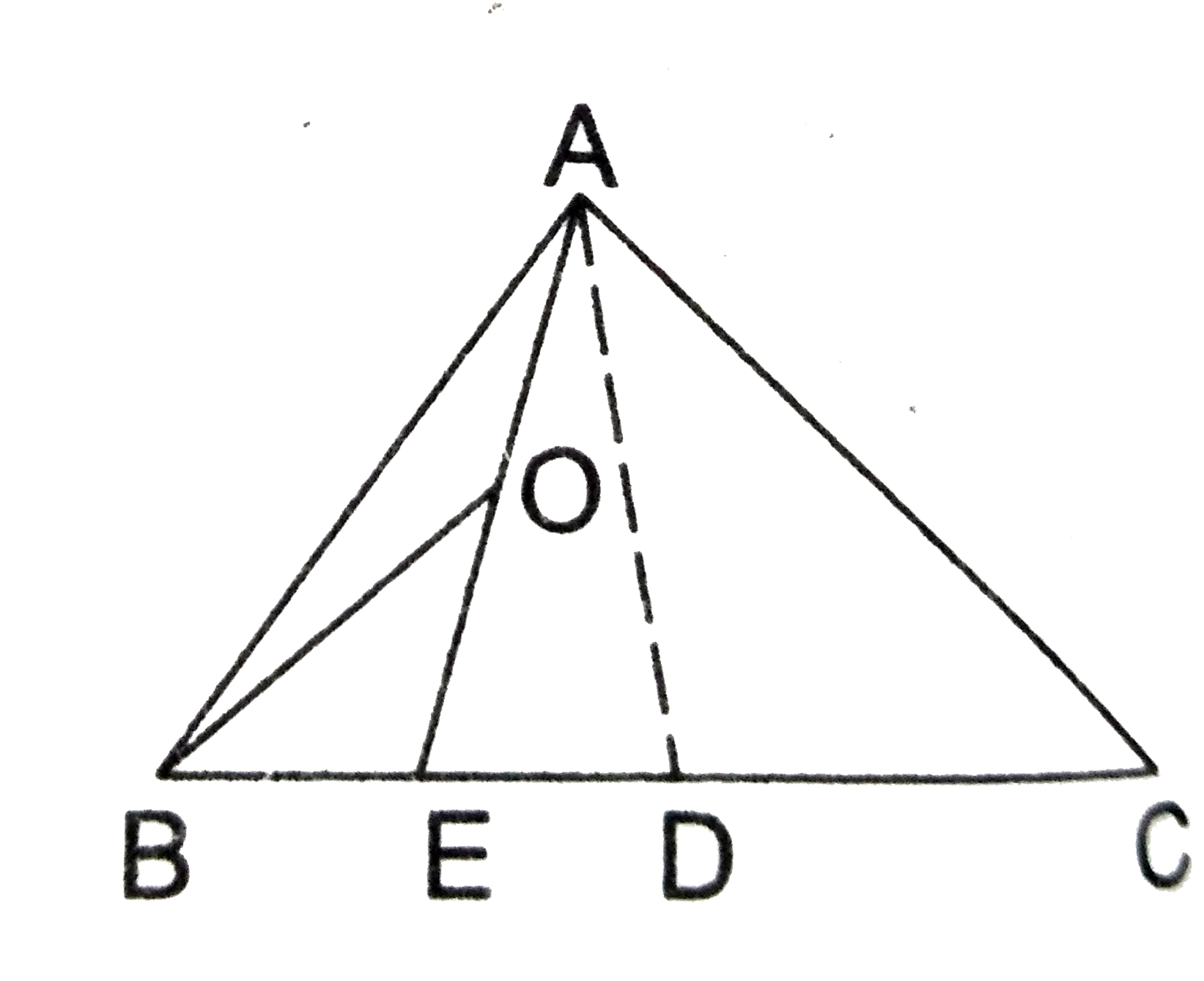 View Solution
View SolutionIn triangle ABC,D is the midpoint of AB, E is the midpoint of DB and F is the midpoint of BC. If the area of ΔABC is 96, the area of ΔAEF is
View SolutionArea of ΔABC=30cm2. D and E are the mid - points of BC and AB respectively. Find A(ΔBDE) :
View SolutionThe area of △ABC is 8cm2 in which AB=AC=4cm and ∠A=90∘.
View Solution

