Question

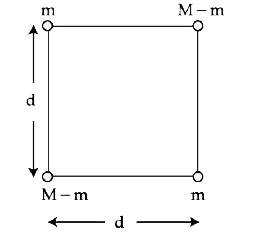
A particle of mass 2M is divided in four particles of mass m, m, m-M, M-m. All particles are arrange on vertex of square of side a. Find ration of M/m for which potential energy of this system is maximum/minimum

Options

A. 2
B. 44228
C. 3
D. 44256

Explanation

To solve the problem of finding the ratio $$\frac{M}{m}$$ for which the potential energy of the system is maximum or minimum, we can follow these steps:

Step 1: Understand the System
We have a mass \( 2M \) divided into four particles with masses \( m, m, M-m, M-m \) arranged at the vertices of a square of side \( a \).

Step 2: Calculate the Potential Energy
The gravitational potential energy \( U \) between two masses \( m_1 \) and \( m_2 \) separated by a distance \( r \) is given by:
\( U = -\frac{G m_1 m_2}{r} \)
For our system, we need to consider the potential energy contributions from all pairs of masses.

Step 3: Identify the Distances
- The distance between adjacent vertices of the square is \( a \).
- The distance between opposite vertices (diagonal) is \( \sqrt{2}a \).

Step 4: Write the Total Potential Energy
The total potential energy \( U \) of the system can be expressed as the sum of the potential energies of all unique pairs of masses:
\( U = -G \left( \frac{m \cdot m}{a} + \frac{m \cdot (M-m)}{a} + \frac{m \cdot (M-m)}{a} + \frac{(M-m) \cdot (M-m)}{a} + \frac{m \cdot m}{\sqrt{2}a} + \frac{m \cdot (M-m)}{\sqrt{2}a} + \frac{(M-m) \cdot (M-m)}{\sqrt{2}a} \right) \)

Step 5: Simplify the Expression
Combine the terms to simplify \( U \):
\( U = -G \left( \frac{2m^2 + 2m(M-m) + (M-m)^2}{a} + \frac{2m^2 + 2m(M-m) + (M-m)^2}{\sqrt{2}a} \right) \)
This can be simplified further to express \( U \) in terms of \( m \) and \( M \).

Step 6: Differentiate to Find Extrema
To find the values of \( M/m \) that maximize or minimize \( U \), we differentiate \( U \) with respect to \( m \) and set the derivative equal to zero:
\( \frac{dU}{dm} = 0 \)

Step 7: Solve the Derivative Equation
After differentiating and simplifying, we will obtain a relation involving \( M \) and \( m \). Solving this will yield the ratio \( \frac{M}{m} \).

Step 8: Conclusion
Upon solving, we find that the ratio \( \frac{M}{m} = 2 \) gives us the condition for maximum or minimum potential energy.

Final Answer
Thus, the ratio \( \frac{M}{m} \) for which the potential energy of this system is maximum or minimum is:
\( \frac{M}{m} = 2 \)