Points E and F respectively lie on sides PQ and PR of ΔPQR. For condition given below state whether EF∣∣QR
PE = 4 cm, QE = 4.5 cm, PF = 8 cm and RF = 9 cm
To determine whether line segment EF is parallel to line segment QR in triangle PQR, we will apply the Basic Proportionality Theorem (BPT). According to BPT, if a line segment is drawn parallel to one side of a triangle, it divides the other two sides proportionally.
1. Identify the Given Lengths:
- PE = 4 cm
- QE = 4.5 cm
- PF = 8 cm
- RF = 9 cm
2. Set Up the Proportions:
According to the BPT, we need to check if:
PEQE=PFRF
3. Calculate the Ratios:
- Calculate PEQE:
PEQE=44.5=44.5=89
- Calculate PFRF:
PFRF=89
4. Compare the Ratios:
Now we compare the two ratios:
PEQE=89andPFRF=89
Since both ratios are equal, we can conclude that:
PEQE=PFRF
5. Conclusion:
Since the ratios are equal, by the Basic Proportionality Theorem, we can conclude that:
EF∥QR
- PE = 4 cm
- QE = 4.5 cm
- PF = 8 cm
- RF = 9 cm
According to the BPT, we need to check if:
PEQE=PFRF
- Calculate PEQE:
PEQE=44.5=44.5=89
PFRF=89
Now we compare the two ratios:
PEQE=89andPFRF=89
Since both ratios are equal, we can conclude that:
PEQE=PFRF
Since the ratios are equal, by the Basic Proportionality Theorem, we can conclude that:
EF∥QR
Topper's Solved these Questions
- CONGRUENCE AND SIMILAR TRIANGLES BOOK - LUCENT PUBLICATIONCHAPTER - CONGRUENCE AND SIMILAR TRIANGLES EXERCISE - EXERCISE-5A
47 Videos
- CONGRUENCE AND SIMILAR TRIANGLES BOOK - LUCENT PUBLICATIONCHAPTER - CONGRUENCE AND SIMILAR TRIANGLES EXERCISE - EXERCISE-5B
8 Videos
- CIRCLE AND ITS TANGENT LINESBOOK - LUCENT PUBLICATIONCHAPTER - CIRCLE AND ITS TANGENT LINESEXERCISE - EXERCISE 8B
27 Videos
- ELEMENTARY TRIGONOMETRIC IDENTITIES BOOK - LUCENT PUBLICATIONCHAPTER - ELEMENTARY TRIGONOMETRIC IDENTITIES EXERCISE - EXERCISE 11B
37 Videos
Similar Questions
Points E and F respectively lie on sides PQ and PR of ΔPQR. For condition given below state whether EF∣∣QR
PE = 3.9 cm, EQ = 3 cm, PF = 3.6 cm and FR = 2.4 cm
View SolutionE and F are points on the sides PQ and PR respectively of ΔPQR. For each of the following cases, state whether EF || QR:
(i) PE = 3.9 cm. EQ = 3 cm. PF = 3.6 cm and FR = 2.4
(ii) PE = 4 cm. QE = 4.5 cm. PF = S cm and RF = 9 cm
(iii) PQ = 1.28 cm, PR = 2.56 cm, PE = 0.18 cm and PF = 0.36 cm
View Solution
Knowledge Check
ABCD is a trapizium with AB∣∣DC. E and F are points on non - parallel sides AD and BC respecitively such that EF∣∣AB, If AE = 3cm, ED = 4.8 cm, BF = 1.5 cm, then the value of CF is :
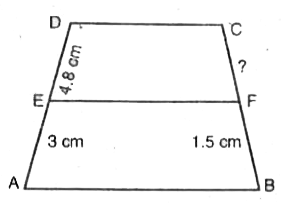 A4.5 cmB2.4 cmC6.0 cmDNone of these
A4.5 cmB2.4 cmC6.0 cmDNone of these
E and F are points on the sides PQ and PR respectively of a ΔPQR. Show that Ef||QR. If PQ = 1.28 cm,PR= 2.56 cm,PE = 0.18 cm and PF= 0.36 cm.
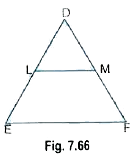
View SolutionL and M are points on the sides DE and DF respectively of a MJEF. State whether LM II EF or not.
DE = 8 cm, DF = 15 cm, LE = 3.2 cm and MF= 6 cm.
View SolutionA and B are respectively the points on the sides PQ and PR of a ΔPQR such that PQ =12.5 cm, PA= 5 cm, BR = 6 cm and PB = 4 cm. Is AB || QR? Give reason for your answer.
View SolutionPE=4m,QE=4.5m,PF=8mandRF=9m.
Is EF∣∣QR? Justify your answer.
View SolutionM and N are points on sides AC and BC respectively of a △ABC. State whether MN||BC if CM = 4.2 cm, MA= 2.8 cm , NB = 3.6 cm, CN = 5.7 cm.
View SolutionConstruct a △PQR in which PQ=5.3 cm. PR = 4.6 cm and QR = 3.8 cm.
View SolutionIn Fig. 9.21, if PR = 12 cm, QR = 6 cm and PL = 8 cm, then QM is

View Solution
