In ΔABC line PQ is drawn parallel to side BC where P and Q are respectively lie on side AB and AC. If AB = 3AP, what is the ratio of area of ΔAPQ to area of ΔABC ?
a)1:3
b)1:5
c)1:7
d)1:9
The correct Answer is:D
To find the ratio of the area of triangle ΔAPQ to the area of triangle ΔABC, we can follow these steps:
Step 1: Understand the Given Information
We are given that line PQ is drawn parallel to side BC of triangle ABC, and points P and Q lie on sides AB and AC respectively. We also know that AB=3AP.
Step 2: Establish the Ratios of the Sides
Since PQ is parallel to BC, triangles APQ and ABC are similar by the Basic Proportionality Theorem (or Thales's theorem).
From the given information, we can express the lengths:
- Let AP=x.
- Then AB=AP+PB=x+3x=4x (since AB=3AP).
Thus, the ratio of the lengths AP to AB is:
APAB=x4x=14
Step 3: Use the Property of Similar Triangles
The areas of similar triangles are proportional to the square of the ratio of their corresponding sides. Therefore, the ratio of the areas of triangles APQ and ABC can be expressed as:
Area(ΔAPQ)Area(ΔABC)=(APAB)2
Step 4: Substitute the Ratio
Substituting the ratio we found:
Area(ΔAPQ)Area(ΔABC)=(14)2=116
Step 5: Conclusion
Thus, the ratio of the area of triangle ΔAPQ to the area of triangle ΔABC is:
Area(ΔAPQ)Area(ΔABC)=116
Final Answer
The ratio of the area of ΔAPQ to the area of ΔABC is 1:16.
---
We are given that line PQ is drawn parallel to side BC of triangle ABC, and points P and Q lie on sides AB and AC respectively. We also know that AB=3AP.
Since PQ is parallel to BC, triangles APQ and ABC are similar by the Basic Proportionality Theorem (or Thales's theorem).
- Let AP=x.
- Then AB=AP+PB=x+3x=4x (since AB=3AP).
APAB=x4x=14
The areas of similar triangles are proportional to the square of the ratio of their corresponding sides. Therefore, the ratio of the areas of triangles APQ and ABC can be expressed as:
Area(ΔAPQ)Area(ΔABC)=(APAB)2
Substituting the ratio we found:
Area(ΔAPQ)Area(ΔABC)=(14)2=116
Thus, the ratio of the area of triangle ΔAPQ to the area of triangle ΔABC is:
Area(ΔAPQ)Area(ΔABC)=116
The ratio of the area of ΔAPQ to the area of ΔABC is 1:16.
Topper's Solved these Questions
- BOOK - LUCENT PUBLICATIONCHAPTER - CONGRUENCE AND SIMILAR TRIANGLES EXERCISE - EXERCISE-5B8videos
CONGRUENCE AND SIMILAR TRIANGLES
- BOOK - LUCENT PUBLICATIONCHAPTER - CONGRUENCE AND SIMILAR TRIANGLES EXERCISE - EXERCISE-5B8videos
CONGRUENCE AND SIMILAR TRIANGLES
- BOOK - LUCENT PUBLICATIONCHAPTER - CIRCLE AND ITS TANGENT LINESEXERCISE - EXERCISE 8B27videos
CIRCLE AND ITS TANGENT LINES
- BOOK - LUCENT PUBLICATIONCHAPTER - ELEMENTARY TRIGONOMETRIC IDENTITIES EXERCISE - EXERCISE 11B37videos
ELEMENTARY TRIGONOMETRIC IDENTITIES
Similar Questions
Knowledge Check
- Question 1 - Select One
In ΔABC,DE∣∣BC where D and E are respectively lie on AB and AC and DE:BC=3:5. What is the ratio of area of triangle ABC to area of triangle DAE ?
A3:1B5:3C9:2D25:9 - Question 2 - Select One
In two isosceles ΔABC and ΔPQR, the ratio of sides AB : PQ is 1 : 3. Find the ratio of area of ΔABC and area of ΔPQR.
AA)1:3BB)1:9CC)9:1DD)3:1 - Question 3 - Select One
In ΔABC, D and E are the points of sides AB and BC respectively such that DE || AC and AD : DB = 3:2. The ratio of area of trapezium ΔCEDA to that of ΔBED is
A4:15B15:4C4:21D21:4
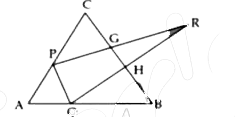
In the given figure, P and Q are the mid points of AC and AB also PG = GR and HQ = HR. What is the ratio of area of ∠PQR : area of ΔABC?
 View Solution
View Solutionin ΔABC, a line parallel to side BC cuts the side AB and AC at points D and E respectively and also point D divide AB in the ratio of 1:4. If area of ΔABC is 200 cm2, then what is the area (in cm2) of quadrilateral DECB?
View SolutionA line parallel to side BC of ΔABC meets AB and AC respectively at P and Q. If AP=QC,PB=4 unit and AQ=9 unit, then length of AP is
View SolutionIn triangle ΔABC, points E and F lie on sides AB and AC such that EF∣∣BC. If EF:BC=3:7 then what is the ratio of areas of ΔAEF and trapezium EBCF ?
View SolutionIn ΔABC, the line parallel to BC Intersects AB and AC at P and Q respectively. If AB:AP=5:3then AQ:QCis :
View Solution
