In a region if electric field is 6V/m then magnetic field will be?
To find the magnetic field in a region where the electric field is given as 6 V/m, we can use the relationship between the electric field (E) and the magnetic field (B) in electromagnetic waves. The relationship is given by the equation:
EB=c
where c is the speed of light in a vacuum, approximately 3×108m/s.
1. Identify the given values:
- Electric field E=6V/m
- Speed of light c=3×108m/s
2. Use the relationship between E and B:
- Rearranging the equation EB=c gives:
B=Ec
3. Substitute the known values into the equation:
B=6V/m3×108m/s
4. Calculate the magnetic field:
- Performing the division:
B=63×108=2×10−8T
5. Final answer:
- The magnetic field B is 2×10−8T (Tesla).
Summary:
The magnetic field in the region where the electric field is 6 V/m is 2×10−8T.
- Electric field E=6V/m
- Speed of light c=3×108m/s
- Rearranging the equation EB=c gives:
B=Ec
B=6V/m3×108m/s
- Performing the division:
B=63×108=2×10−8T
- The magnetic field B is 2×10−8T (Tesla).
The magnetic field in the region where the electric field is 6 V/m is 2×10−8T.
Similar Questions
A plane electromagnetic wave with frequency of 30 MHz travels in free space. At particular point in space and time, electric field is 6 V/m. The magnetic field at this point will be x×10−8T. The value of x is ________
View SolutionIn a region of crossed fields as shown, the strength of electric field is E and that of magnetic field is B. Three positively charged particles with speeds V1,V2andV3 are projected and their paths are shown. From this it implies that
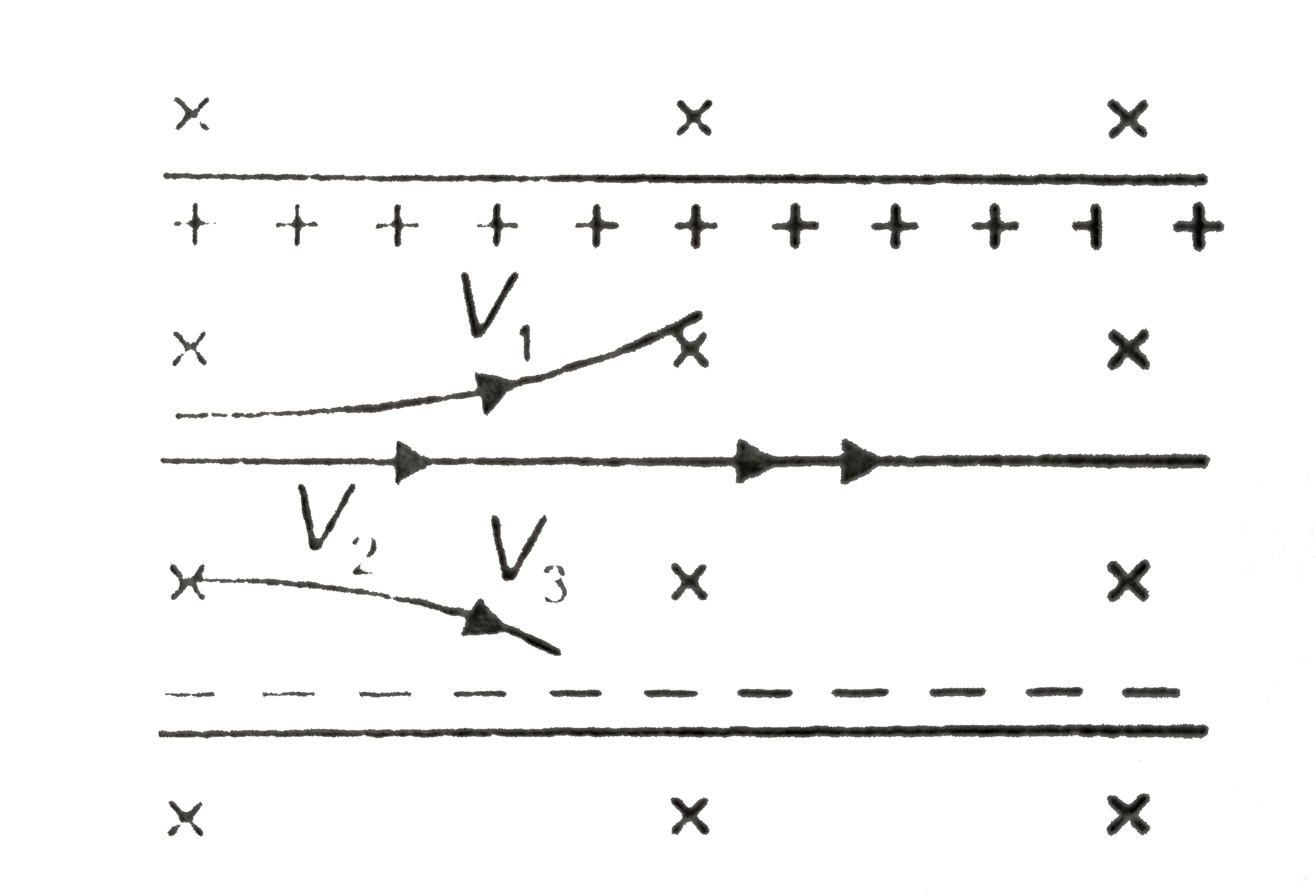
View Solution
Knowledge Check
A charge q moves in a region where electric field E and the magnetic field B both exist, then the force on its is
Aq(v×B)BqE+q(v×B)CqB+q(B×v)DqB+q(E×v)In a certain region of space electric field E and magnetic field B are perpendicular ot each other and an electron enters region perpendicular to the direction of B and E both and moves undeflected, then velocity of electron is
A∣∣→E∣∣∣∣→B∣∣B→E×→BC∣∣→B∣∣∣∣→E∣∣D→E.→BA charge particle travels along a straight line with a speed v in region where both electric field E and magnetic field b are present.It follows that
A|E|=|B| and the two field are perpendicularB|E|=v|B| and the two field are perpendicularC|B|=v|E| and the two field are parallelD|B|=v|E| and the two fields are perpendicular
Induced electric field due to changing magnetic field
View SolutionA beam of proton passes undeflected with a horizontal velocity v, through a region of electric and magnetic fields, mutually perpendicular to each other and perpendicular to the direction of the beam. If the magnitudes of the electric and magnetic fields are 100kV/m, 50mT respectively, calculate the velocity of the beam v.
View SolutionElectric field induced by changing magnetic fields are
View SolutionForce acting on a moving charged particle in a region of electric and magnetic fields is called
View SolutionIn a region where both non-zero uniform electric field and magnetic field coexist, the path of a charged particle
View Solution