The solution of linear inequalities x+y≥5andx−y≤3 lies
Only in the first quadrant
In the first and second quadrants
In the second and third quadrants
In the third and fourth quadrants
To solve the linear inequalities x+y≥5 and x−y≤3, we will use a graphical method. Here is the step-by-step solution:
Step 1: Graph the first inequality x+y≥5
1. Convert to equality: Start by rewriting the inequality as an equation:
x+y=5
2. Find intercepts:
- When x=0, y=5 (Point: (0,5))
- When y=0, x=5 (Point: (5,0))
3. Draw the line: Plot the points (0,5) and (5,0) on the graph and draw a straight line through them. Since the inequality is ≥, shade the area above the line.
x+y=5
2. Find intercepts:
- When x=0, y=5 (Point: (0,5))
- When y=0, x=5 (Point: (5,0))
3. Draw the line: Plot the points (0,5) and (5,0) on the graph and draw a straight line through them. Since the inequality is ≥, shade the area above the line.
Similar Questions
Knowledge Check
The graphical solution of linear inequalities x+y≥5 and x−y≤3,
A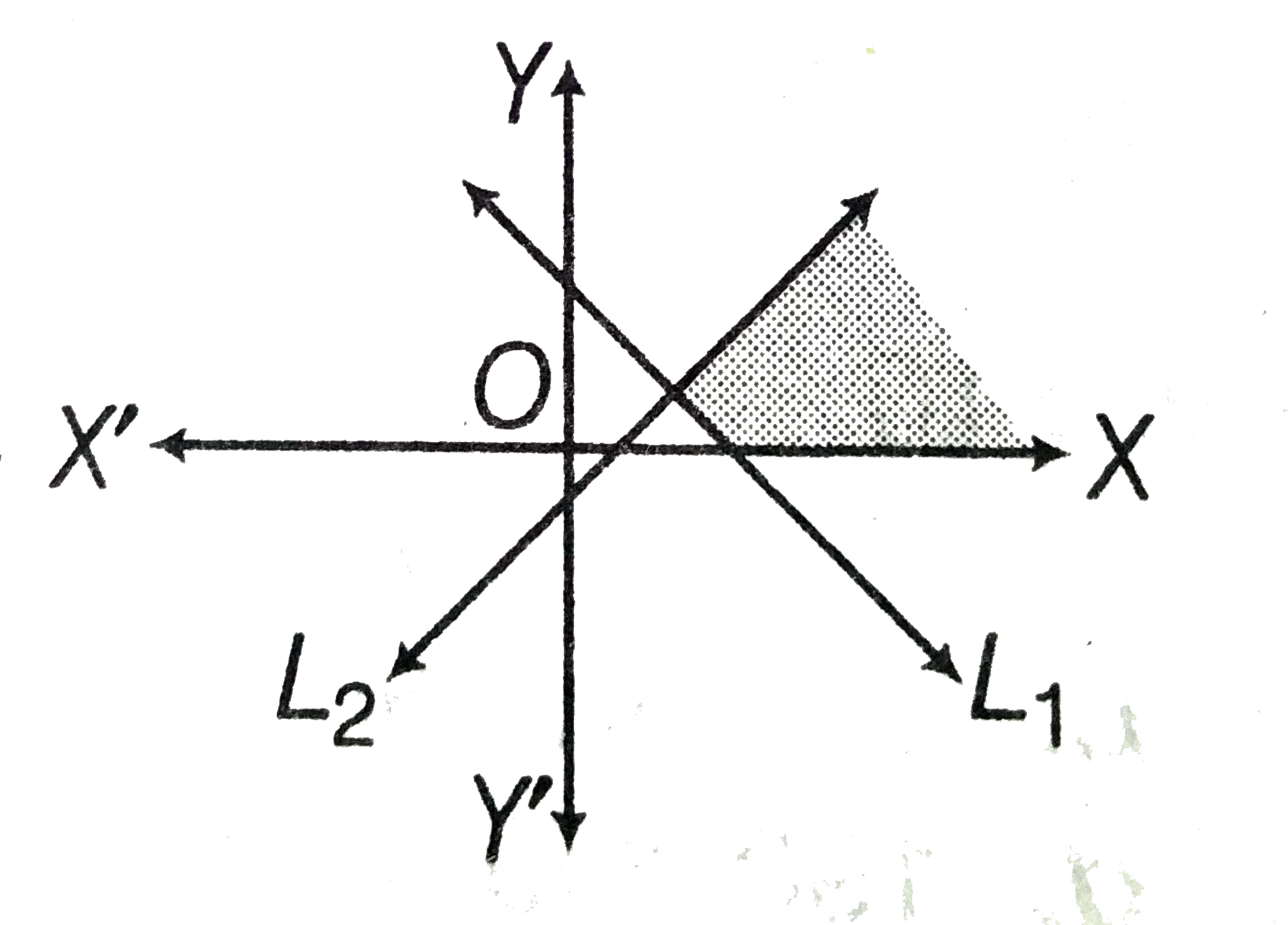 B
B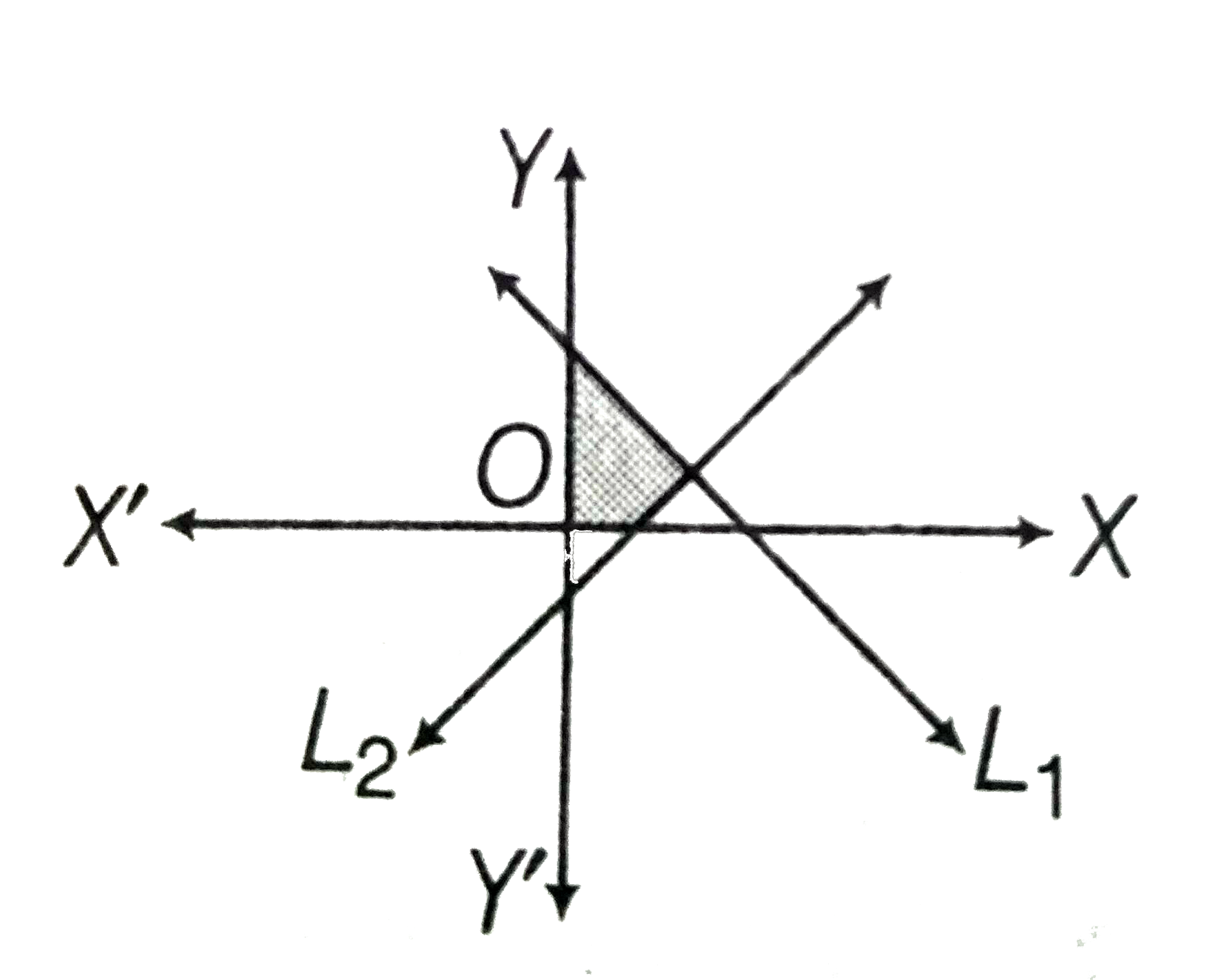 C
C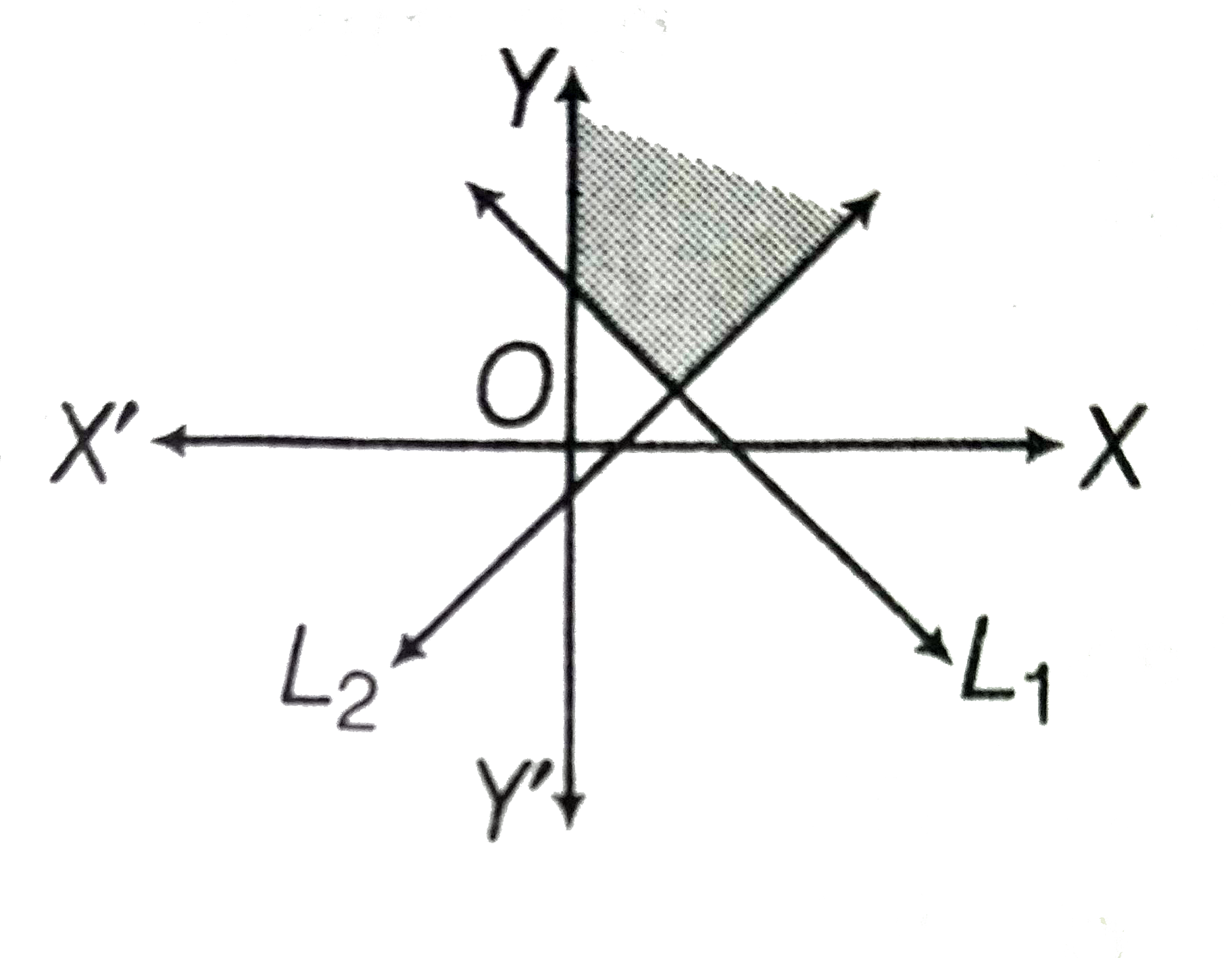 D
D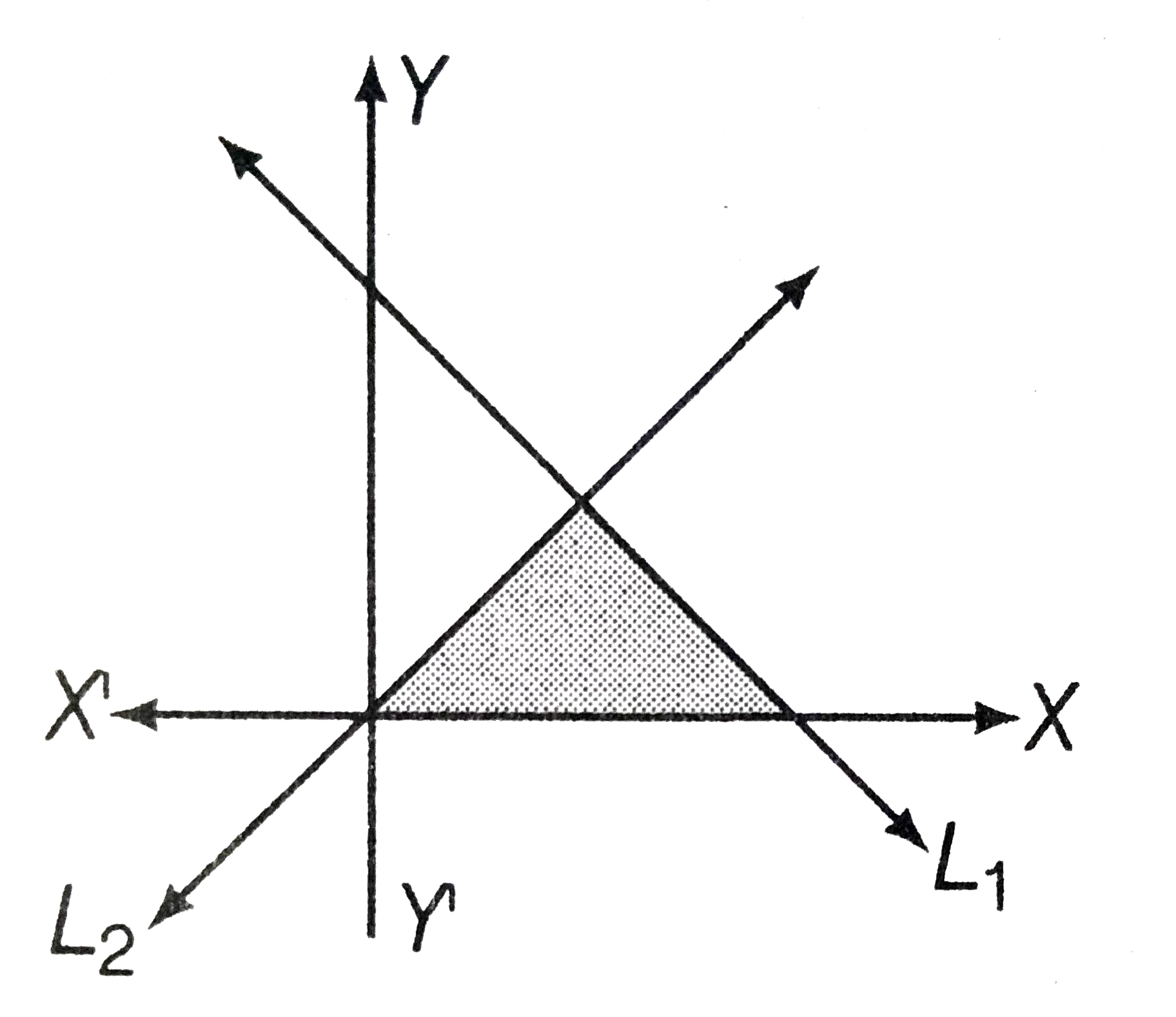
The solution set of the inequation x+2y≥3 is
Ahalf plane containing the originBhalf plane not containing the originCthe whole XY-plane except point lying on line x+2y−3=0Dopen half plane not containing the originThe solution of the linear inequality 2x+5x−1>5 is
A1<x<103B−1<x<103C2<x<103DNone of these
The solution set of linear constraints x−2y≥0,2x−y≤−2 and x,y≥0 is
View SolutionThe vertex of common graph of inequalities 2x+y≥2andx−y≤3 , is
View SolutionThe graphical solution of the inequalities x+2y≤10,x+y≥1,x−y≤0,x≥0,y≥0 is
View SolutionSolution set of the inequality y≤0 is
View SolutionThe solution set of the inequations x≤4,x−y≥0,3x+y≥0
View Solution
